练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    曲线在点处的切线与x轴交点的横坐标为an．
    （1）求an；
    （2）设，求数到的前n项和Sn．

    （1） ；（2）.

    解析试题分析：（1）
    切线方程为
    令                           4分
    （2）
                                6分
                10分
    从而                            12分
    考点：本题主要考查导数的几何意义，数列的通项公式，“错位相减法”。
    点评：中档题，本题综合考查导数的几何意义，数形结合思想，数列的通项公式及“错位相减法”求和，难度适中。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （1）设，试比较与的大小；
    （2）是否存在常数，使得对任意大于的自然数都成立？若存在，试求出的值并证明你的结论；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数f(x)＝(1＋x)2－2ln (1＋x)．
    (1)求函数f(x)的单调区间；
    (2)若关于x的方程f(x)＝x2＋x＋a在[0,2]上恰有两个相异实根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，
    （1）若x=1时取得极值，求实数的值；
    （2）当时，求在上的最小值；
    （3）若对任意，直线都不是曲线的切线，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交3元的管理费，预计当每件产品的售价为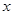元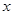（∈[7,11]）时，一年的销售量为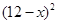万件．
    （1）求分公司一年的利润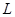（万元）与每件产品的售价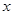的函数关系式；
    （2）当每件产品的售价为多少元时，分公司一年的利润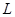最大，并求出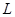的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）若函数在上为增函数，求实数的取值范围；
    （2）当时，求在上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数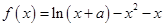在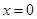处取得极值.
    (1)求实数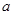的值；
    (2)若关于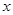的方程在区间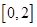上恰有两个不同的实数根,求实数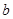的取值范围；
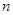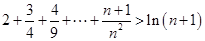    (3)证明:对任意的正整数,不等式都成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知的图像在点处的切线与直线平行.
    （1）求a，b满足的关系式；
    （2）若上恒成立，求a的取值范围；
    （3）证明：（）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，（，为常数，），且这两函数的图像有公共点，并在该公共点处的切线相同.
    （Ⅰ）求实数的值；
    （Ⅱ）若时，恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案