
科目:高中数学 来源: 题型:选择题
| A. | x2+1≥2|x|(x∈R) | B. | lg(x2+$\frac{1}{4}$)>lgx(x>0) | ||
| C. | sinx+$\frac{1}{sinx}$≥2(x≠kπ,k∈Z) | D. | $\frac{1}{{x}^{2}+1}$<1(x∈R) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sinxcosx | B. | y=sin(2x+$\frac{π}{2}$) | C. | y=tan2x | D. | y=sin2x+cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
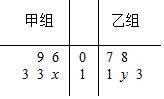 为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )
为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com