
【题目】已知点![]() ,
,![]() 是函数
是函数![]() 的图象上任意不同两点,依据图象可知,线段
的图象上任意不同两点,依据图象可知,线段![]() 总是位于
总是位于![]() ,
,![]() 两点之间函数图象的上方,因此有结论
两点之间函数图象的上方,因此有结论![]() 成立.运用类比思想方法可知,若点
成立.运用类比思想方法可知,若点![]() ,
,![]() 是函数
是函数![]() 的图象上任意不同两点,则类似地有__________成立.
的图象上任意不同两点,则类似地有__________成立.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;以D为起点,其余顶点为终点的向量分别为
;以D为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .若m、M分别为(
.若m、M分别为( ![]() +
+ ![]() +
+ ![]() )(
)( ![]() +
+ ![]() +
+ ![]() )的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
)的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
A.m=0,M>0
B.m<0,M>0
C.m<0,M=0
D.m<0,M<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行;
B. 若两个平面平行,则分别位于这两个平面的直线也互相平行;
C. 平行于同一个平面的两个平面平行;
D. 若两个平面平行,则其中一个平面内的直线平行于另一个平面;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2019年举行促销活动,经过调查测算,该产品的年销量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (
(![]() )(单位:万元)满足
)(单位:万元)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).
为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).
(1)将该厂家2019年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2019年的年促销费用投入多少万元时,厂家利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH. 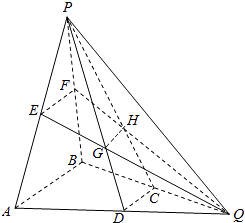
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com