
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论k的范围,确定函数的单调区间即可;
(Ⅲ)令$g(x)=ln(x+1)+\frac{1}{x+1}-1$,求出函数的导数,根据函数的单调性证明结论即可.
解答 解:(Ⅰ)当k=0时,f(x)=ln(1+x)-x,则f(1)=ln2-1
所以$f'(x)=\frac{1}{1+x}-1$,则$f'(1)=-\frac{1}{2}$…(2分)
所以y-f(1)=f'(1)(x-1),即x+2y-2ln2+1=0…(4分)
(Ⅱ)由已知x>-1,$f'(x)=\frac{1}{1+x}-1+kx$,即$f'(x)=\frac{x(kx+k-1)}{1+x}$,
当k=0时,$f'(x)=\frac{1}{1+x}-1=-\frac{x}{1+x}$,因为x>-1
所以在(-1,0)上增,在(0,+∞)上减…(5分)
当0<k<1时,由$f'(x)=\frac{x(kx+k-1)}{1+x}=0$,得x1=0,${x_2}=\frac{1-k}{k}>0$
所以在(-1,0)和$(\frac{1-k}{k},+∞)$上f'(x)>0;在$(0,\frac{1-k}{k})$上f'(x)<0
故f(x)在(-1,0)和$(\frac{1-k}{k},+∞)$单调递增,在$(0,\frac{1-k}{k})$单调递减…(7分)
当k>1时,$f'(x)=\frac{x(kx+k-1)}{1+x}=0$,得${x_1}=\frac{1-k}{k}∈(-1,0)$,x2=0.
所以在$(-1,\frac{1-k}{k})$和(0,+∞)上f'(x)>0;在$(\frac{1-k}{k},0)$上f'(x)<0
故f(x)单调递增区间是$(-1,\frac{1-k}{k})$和(0,+∞),减区间是$(\frac{1-k}{k},0)$…(9分)
(Ⅲ)令$g(x)=ln(x+1)+\frac{1}{x+1}-1$,则$g'(x)=\frac{1}{x+1}-\frac{1}{{{{(x+1)}^2}}}$=$\frac{x}{{{{(x+1)}^2}}}$.…(11分)
所以 当x∈(-1,0)时,g'(x)<0,当x∈(0,+∞)时,g'(x)>0.
所以 当x>-1时,g(x)≥g(0),即 $ln(x+1)+\frac{1}{x+1}-1$≥0
所以 $ln(x+1)≥1-\frac{1}{x+1}$.…(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
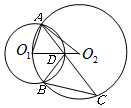 如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.
如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20人 | B. | 15人 | C. | 10人 | D. | 5人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com