
【题目】已知直线l与抛物线![]() 交于点A,B两点,与x轴交于点M,直线OA,OB的斜率之积为
交于点A,B两点,与x轴交于点M,直线OA,OB的斜率之积为![]() .
.
(1)证明:直线AB过定点;
(2)以AB为直径的圆P交x轴于E,F两点,O为坐标原点,求|OE|![]() |OF|的值.
|OF|的值.
科目:高中数学 来源: 题型:
【题目】(本题满分13分)
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为![]() 元(
元(![]() 为常数,且
为常数,且![]() ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为![]() 元(
元(![]() ),根据市场调查,销售量
),根据市场调查,销售量![]() 与
与![]() 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润![]() 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)若![]() ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价![]() 为多少元时,该工厂的利润
为多少元时,该工厂的利润![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设斜率为k(k>0)的直线l与椭圆C: ![]() +
+ ![]() =1交于A、B两点,且OA⊥OB.
=1交于A、B两点,且OA⊥OB. 
(Ⅰ)求直线l在y轴上的截距(用k表示);
(Ⅱ)求△AOB面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过左焦点任作直线l,交椭圆的上半部分于点M,当l的斜率为
,过左焦点任作直线l,交椭圆的上半部分于点M,当l的斜率为 ![]() 时,|FM|=
时,|FM|= ![]() .
.
(1)求椭圆C的方程;
(2)椭圆C上两点A,B关于直线l对称,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.
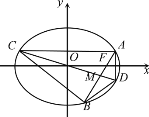
(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]() 的焦点分别为
的焦点分别为![]() ,
, ![]() 交于O,A两点(O为坐标原点),且
交于O,A两点(O为坐标原点),且![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点O的直线交![]() 的下半部分于点M,交
的下半部分于点M,交![]() 的左半部分于点N,点
的左半部分于点N,点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(ax﹣
sin(ax﹣ ![]() )cos(ax﹣
)cos(ax﹣ ![]() )+2cos2(ax﹣
)+2cos2(ax﹣ ![]() )(a>0),且函数的最小正周期为
)(a>0),且函数的最小正周期为 ![]() .
.
(Ⅰ)求a的值;
(Ⅱ)求f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e
,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e ![]() e
e ![]() 的最大值为( )
的最大值为( )
A.![]()
B.2(ln2﹣1)
C.![]()
D.ln2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com