
 ,设随机变量
,设随机变量 .
. 的可能取值,并求随机变量
的可能取值,并求随机变量 的最大值;
的最大值; 取得最大值”的概率;
取得最大值”的概率; 的分布列和数学期望与方差.
的分布列和数学期望与方差. 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
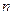 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这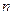 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮 测试中的两次排序的偏离程度的高低为其评为。
测试中的两次排序的偏离程度的高低为其评为。 ,分别以
,分别以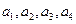 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令 ,
,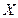 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。 (Ⅰ)写出
(Ⅰ)写出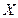 的可能值集合;
的可能值集合;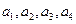 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求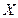 的分布列;
的分布列; ,
,查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.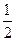 , ,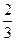 | B.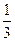 , ,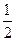 | C.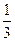 , ,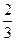 | D.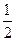 , ,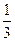 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com