
 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.科目:高中数学 来源:不详 题型:解答题
 如下:若是白色,则
如下:若是白色,则 ;若是黄色,则
;若是黄色,则 ;若是红色,则
;若是红色,则 ;若卡片数字是
;若卡片数字是 ,则
,则

 与数字方差
与数字方差
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求 的分布列。
的分布列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,设随机变量
,设随机变量 .
. 的可能取值,并求随机变量
的可能取值,并求随机变量 的最大值;
的最大值; 取得最大值”的概率;
取得最大值”的概率; 的分布列和数学期望与方差.
的分布列和数学期望与方差.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
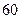 名学生,将其成绩(百分制)(均为整数)分成六段
名学生,将其成绩(百分制)(均为整数)分成六段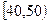 ,
,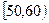 …
…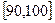 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: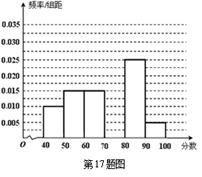
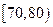 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;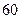 名学生中
名学生中 随机抽取
随机抽取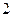 人,抽到的学生成绩在
人,抽到的学生成绩在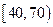 记
记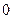 分,在
分,在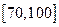 记
记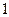 分,用
分,用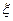 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求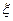 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、
、 、
、 ,投掷时,A、B两枚正面向上的概率为分别为
,投掷时,A、B两枚正面向上的概率为分别为 ,另两枚C、D正面向上的概率分别为
,另两枚C、D正面向上的概率分别为
 .这四枚纪念币同时投掷一次,设
.这四枚纪念币同时投掷一次,设 表示出现正面向上的枚数。
表示出现正面向上的枚数。 的值;
的值; 的分布列及数学期望(用
的分布列及数学期望(用 表示);
表示); 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com