
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:不详 题型:解答题
 个球,求
个球,求 的分布列及期望
的分布列及期望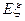 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题:
时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题: 的分布列和期望;
的分布列和期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
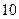 里
里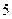 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到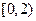 、
、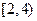 、
、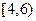 、
、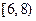 、
、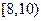 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;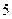 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.| 下午开始上课时间 | 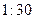 | 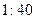 | 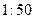 | 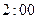 | 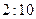 |
| 平均每天午休人数 | 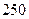 | 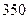 | 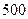 | 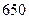 | 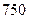 |
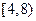 的概率是多少?
的概率是多少?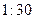 作为横坐标
作为横坐标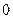 ,然后上课时间每推迟
,然后上课时间每推迟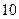 分钟,横坐标
分钟,横坐标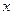 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标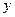 ,试列出
,试列出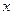 与
与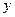 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数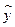 与上课时间
与上课时间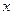 之间的线性回归方程
之间的线性回归方程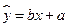 ;
;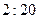 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?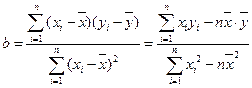 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,分别写在6张小卡片上,放入盒中.
,分别写在6张小卡片上,放入盒中. 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com