
(本小题满分14分)已知直线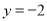 上有一个动点
上有一个动点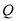 ,过点
,过点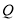 作直线
作直线 垂直于
垂直于 轴,动点
轴,动点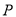 在
在 上,且满足
上,且满足 (
(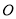 为坐标原点),记点
为坐标原点),记点 的轨迹为
的轨迹为 .
.
(1)求曲线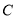 的方程;
的方程;
(2)若直线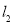 是曲线
是曲线 的一条切线,当点
的一条切线,当点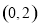 到直线
到直线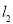 的距离最短时,求直线
的距离最短时,求直线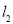 的方程.
的方程.
(1)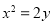 ;(2)
;(2) 或
或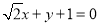 .
.
【解析】
试题分析:本题主要考查抛物线的标准方程、点到直线的距离公式、向量的数量积、均值定理等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问,设出P、Q点坐标,由题意知,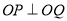 ,利用两直线的斜率相乘为-1,得到曲线C的方程;第二问,设出直线
,利用两直线的斜率相乘为-1,得到曲线C的方程;第二问,设出直线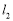 的方程,与曲线C的方程联立,由于直线
的方程,与曲线C的方程联立,由于直线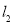 是曲线
是曲线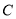 的一条切线,所以
的一条切线,所以 ,解出
,解出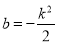 ,再利用点到直线的距离公式求出点
,再利用点到直线的距离公式求出点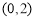 到直线
到直线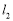 的距离d,利用均值定理求出d的最小值,并求出等号成立的条件,即k的值,从而得到直线
的距离d,利用均值定理求出d的最小值,并求出等号成立的条件,即k的值,从而得到直线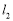 的方程.
的方程.
试题解析:(1)设点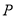 的坐标为
的坐标为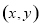 ,则点
,则点 的坐标为
的坐标为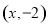 .
.
∵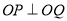 ,
,
∴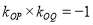 . (或者用向量:
. (或者用向量: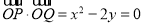 ,且
,且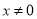 得出)
得出)
当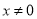 时,得
时,得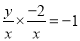 ,化简得
,化简得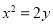 . 2分
. 2分
当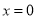 时,
时, 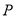 、
、 、
、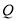 三点共线,不符合题意,故
三点共线,不符合题意,故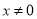 .
.
∴曲线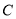 的方程为
的方程为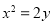
 . 4分
. 4分
(2)解法1:∵ 直线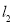 与曲线
与曲线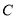 相切,
相切,
∴直线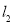 的斜率存在.
的斜率存在.
设直线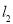 的方程为
的方程为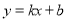 , 5分
, 5分
由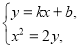 得
得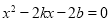 .
.
∵ 直线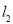 与曲线
与曲线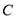 相切, 则
相切, 则 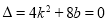 ,即
,即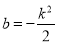 .
.
∴ 直线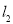 的方程为
的方程为 6分
6分
∴ 点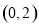 到直线
到直线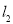 的距离
的距离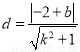
 7分
7分
 8分
8分
 9分
9分
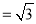 . 10分
. 10分
当且仅当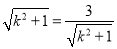 ,即
,即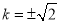 时,等号成立.此时
时,等号成立.此时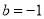 . 12分
. 12分
∴直线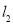 的方程为
的方程为 或
或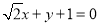 . 14分
. 14分
解法2:由 ,得
,得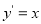 , 5分
, 5分
∵直线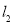 与曲线
与曲线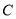 相切, 设切点
相切, 设切点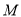 的坐标为
的坐标为 ,其中
,其中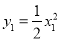 ,
,
则直线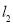 的方程为:
的方程为: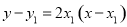 ,化简得
,化简得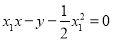 . 6分
. 6分
点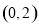 到直线
到直线 的距离
的距离
 7分
7分
 8分
8分
 9分
9分
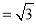 . 10分
. 10分
当且仅当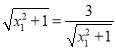 ,即
,即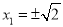 时,等号成立. 12分
时,等号成立. 12分
∴直线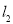 的方程为
的方程为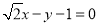 或
或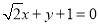 . 14分
. 14分
解法3:由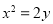 ,得
,得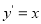 , 5分
, 5分
∵直线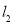 与曲线
与曲线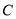 相切, 设切点
相切, 设切点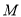 的坐标为
的坐标为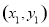 ,其中
,其中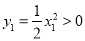 ,
,
则直线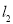 的方程为:
的方程为: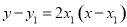 ,化简得
,化简得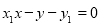 . 6分
. 6分
点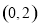 到直线
到直线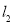 的距离
的距离
 7分
7分
 8分
8分
 9分
9分
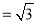 . 10分
. 10分
当且仅当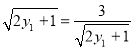 ,即
,即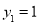 时,等号成立,此时
时,等号成立,此时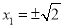 . 12分
. 12分
∴直线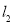 的方程为
的方程为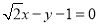 或
或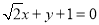 . 14分
. 14分
考点:抛物线的标准方程、点到直线的距离公式、向量的数量积、均值定理.


科目:高中数学 来源:2014-2015学年山西省高三第四次诊断考试文科数学试卷(解析版) 题型:选择题
为得到函数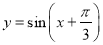 的图象,可将函数
的图象,可将函数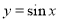 的图象向左平移
的图象向左平移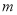 个单位长度,或向右平移
个单位长度,或向右平移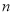 个单位长度(
个单位长度(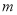 ,
,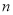 均为正数),则
均为正数),则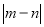 的最小值是( )
的最小值是( )
A.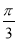 B.
B.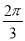 C.
C.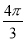 D.
D.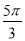
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试文科数学试卷(解析版) 题型:填空题
设复数z满足 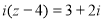 (i是虚数单位),则z的虚部为_______.
(i是虚数单位),则z的虚部为_______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试理科数学试卷(解析版) 题型:填空题
将函数 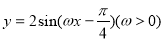 的图象分别向左、向右各平移
的图象分别向左、向右各平移 个单位长度后,所得的两个图象对称轴重合,则
个单位长度后,所得的两个图象对称轴重合,则  的最小值为______.
的最小值为______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试理科数学试卷(解析版) 题型:填空题
某用人单位从甲、乙、丙、丁4名应聘者中招聘2人,若每名应聘者被录用的机会均等,则甲、乙2人中至少有1入被录用的概率为 _______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研文科数学试卷(解析版) 题型:填空题
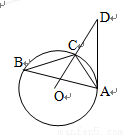
(几何证明选做题)如图,已知 内接于圆
内接于圆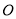 ,点
,点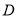 在
在 的延长线上,
的延长线上,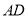 切圆
切圆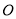 于
于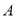 ,若
,若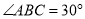 ,
,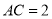 ,则
,则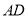 的长为____________.
的长为____________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么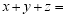 ______.
______.
|
| 3 |
| a |
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com