
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
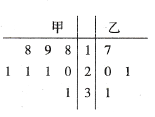
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() (2)
(2)![]() (3)分布列见解析
(3)分布列见解析![]()
【解析】试题分析:
(1)本题求独立事件同时发生的概率,解题时运用对立事件的概率求解比较简单.(2)运用条件概率求解,解题时要分清谁是条件.(3)由题意可得到![]() 的所有可能取值,然后分别求出概率,列成表格的形式可得分布列,根据定义求得期望值.
的所有可能取值,然后分别求出概率,列成表格的形式可得分布列,根据定义求得期望值.
试题解析:
(1)由题意得甲车间的合格零件数为4,乙车间的合格的零件数为2,
故所求概率为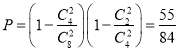 .
.
即甲车间至少一个零件合格且乙车间至少一个零件合格的概率为![]() .
.
(2)设事件![]() 表示“2件合格,2件不合格”;事件
表示“2件合格,2件不合格”;事件![]() 表示“3件合格,1件不合格”;事件
表示“3件合格,1件不合格”;事件![]() 表示“4件全合格”; 事件
表示“4件全合格”; 事件![]() 表示“检测通过”;事件
表示“检测通过”;事件![]() 表示“检测良好”.
表示“检测良好”.
则![]() ,
,
∴![]() .
.
故甲车间在这次检测通过的条件下,获得检测良好的概率为![]() .
.
(3)由题意可得![]() 的所有可能取值为0,1,2.
的所有可能取值为0,1,2.
![]() ,
,
![]() ,
,
![]() .
.
∴ 随机变量![]() 的分布列为
的分布列为
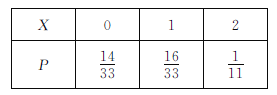
∴![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的焦点为
的焦点为![]() ,过抛物线
,过抛物线![]() 上的动点
上的动点![]() (除顶点
(除顶点![]() 外)作
外)作![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() .过点
.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() (垂足为
(垂足为![]() )与直线
)与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为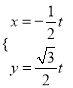 (
(![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)当![]() (
(![]() )时在曲线
)时在曲线![]() 上对应的点为
上对应的点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的极坐标,并判断
点的极坐标,并判断![]() 是否在曲线
是否在曲线![]() 上(其中点
上(其中点![]() 为半圆的圆心)
为半圆的圆心)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() .
.
(Ⅰ)若数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若![]() ,
, ![]() ,且
,且![]() .
.
(i)求![]() 的值;
的值;
(ii)对于数列![]() 和
和![]() ,满足关系式
,满足关系式![]() ,
, ![]() 为常数,且
为常数,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x),且对任意x>0,都有f′(x)>![]() .
.
(1)判断函数F(x)=![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(3)请将(2)中结论推广到一般形式,并证明你所推广的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·郑州第二次质量预测)如图,高为1的等腰梯形ABCD中,AM=CD=![]() AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
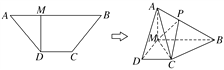
(1)在AB边上是否存在点P,使AD∥平面MPC?
(2)当点P为AB边的中点时,求点B到平面MPC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com