
【题目】已知函数f(x)的导函数f′(x),且对任意x>0,都有f′(x)>![]() .
.
(1)判断函数F(x)=![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(3)请将(2)中结论推广到一般形式,并证明你所推广的结论.
【答案】(1) 见解析;(2) 见解析;(3) 见解析.
【解析】试题分析:(Ⅰ)判断F(x)的单调性,则需对F(x)求导,得F′(x)=![]() ,∵f ′(x)>
,∵f ′(x)>![]() ,x>0,则xf ′(x)-f(x)>0,即F′(x)>0,F(x)=
,x>0,则xf ′(x)-f(x)>0,即F′(x)>0,F(x)=![]() 在(0,+∞)上是增函数.(Ⅱ)要证明f(x1)+f(x2)<f(x1+x2),可以从第(Ⅰ)的结论入手,∵x1>0,x2>0,∴0<x1<x1+x2,F(x)=
在(0,+∞)上是增函数.(Ⅱ)要证明f(x1)+f(x2)<f(x1+x2),可以从第(Ⅰ)的结论入手,∵x1>0,x2>0,∴0<x1<x1+x2,F(x)=![]() 在(0,+∞)上是增函数,则F(x1)<F(x1+x2),即
在(0,+∞)上是增函数,则F(x1)<F(x1+x2),即![]() <
<![]() ,而x1>0,所以f(x1)<
,而x1>0,所以f(x1)<![]() f(x1+x2),同理f(x2)<
f(x1+x2),同理f(x2)<![]() f(x1+x2),两式相加,得f(x1)+f(x2)<f(x1+x2),得证.(Ⅲ)(Ⅱ)中结论的推广形式为:设x1,x2,…,xn∈(0,+∞),其中n≥2,则f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).证明的方法同(Ⅱ)的证明,∵x1>0,x2>0,…,xn>0,∴0<x1<x1+x2+…+xn.F(x)=
f(x1+x2),两式相加,得f(x1)+f(x2)<f(x1+x2),得证.(Ⅲ)(Ⅱ)中结论的推广形式为:设x1,x2,…,xn∈(0,+∞),其中n≥2,则f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).证明的方法同(Ⅱ)的证明,∵x1>0,x2>0,…,xn>0,∴0<x1<x1+x2+…+xn.F(x)=![]() 在(0,+∞)上是增函数,F(x1)<F(x1+x2+…+xn),即
在(0,+∞)上是增函数,F(x1)<F(x1+x2+…+xn),即![]() <
<![]() ,而x1>0,所以f(x1)<
,而x1>0,所以f(x1)<![]() f(x1+x2+…+xn),同理f(x2)<
f(x1+x2+…+xn),同理f(x2)<![]() f(x1+x2+…+xn),……
f(x1+x2+…+xn),……
f(xn)<![]() f(x1+x2+…+xn),以上n个不等式相加,得f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn),得证.
f(x1+x2+…+xn),以上n个不等式相加,得f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn),得证.
试题解析:(Ⅰ)对F(x)求导数,得F′(x)=![]() .
.
∵f ′(x)>![]() ,x>0,∴xf ′(x)>f(x),即xf ′(x)-f(x)>0,
,x>0,∴xf ′(x)>f(x),即xf ′(x)-f(x)>0,
∴F′(x)>0.
故F(x)=![]() 在(0,+∞)上是增函数.
在(0,+∞)上是增函数.
(Ⅱ)∵x1>0,x2>0,∴0<x1<x1+x2.
由(Ⅰ),知F(x)=![]() 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
∴F(x1)<F(x1+x2),即![]() <
<![]() .
.
∵x1>0,∴f(x1)<![]() f(x1+x2).
f(x1+x2).
同理可得f(x2)<![]() f(x1+x2).
f(x1+x2).
以上两式相加,得f(x1)+f(x2)<f(x1+x2).
(Ⅲ)(Ⅱ)中结论的推广形式为:
设x1,x2,…,xn∈(0,+∞),其中n≥2,则f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).
∵x1>0,x2>0,…,xn>0,
∴0<x1<x1+x2+…+xn.
由(Ⅰ),知F(x)=![]() 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
∴F(x1)<F(x1+x2+…+xn),即![]() <
<![]() .
.
∵x1>0,
∴f(x1)<![]() f(x1+x2+…+xn).
f(x1+x2+…+xn).
同理可得
f(x2)<![]() f(x1+x2+…+xn),
f(x1+x2+…+xn),
f(x3)<![]() f(x1+x2+…+xn),
f(x1+x2+…+xn),
……
f(xn)<![]() f(x1+x2+…+xn).
f(x1+x2+…+xn).
以上n个不等式相加,得f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).


科目:高中数学 来源: 题型:
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
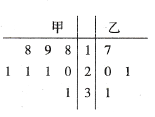
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量![]() 分布在
分布在![]() 内,且销售量
内,且销售量![]() 的分布频率
的分布频率
 .
.
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若销售量大于等于80,则称该日畅销,其余为滞销,根据是否畅销从这50天中用分层抽样的方法随机抽取5天,再从这5天中随机抽取2天,求这2天中恰有1天是畅销日的概率(将频率视为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
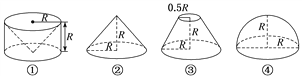
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com