
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为梯形,平面
为梯形,平面![]() 平面
平面![]()
![]()
![]() 为侧棱
为侧棱![]() 的中点,且
的中点,且![]() .
.
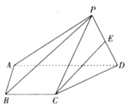
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
![]() 为侧棱
为侧棱![]() 的中点,
的中点, ![]() .,再证四边形
.,再证四边形![]() 为平行四边形,则
为平行四边形,则![]() .故平面
.故平面![]() 平面
平面![]() .
.![]() 平面
平面![]() 平面
平面![]() .
.
(2)解:过点![]() 作
作![]() 于
于![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
![]() .
.
取![]() 的中点
的中点![]() ,如图所示,以
,如图所示,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,
,
求出相应点的坐标和相应向量的坐标,求出平面![]() 的法向量
的法向量![]() 及平面
及平面![]() 的一个法向量
的一个法向量![]() ,再根据二面角
,再根据二面角![]() 为钝角,可得二面角
为钝角,可得二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
![]() 为侧棱
为侧棱![]() 的中点,
的中点, ![]() .
.
![]() 四边形
四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
(2)解:过点![]() 作
作![]() 于
于![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
![]() .
.
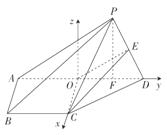
取![]() 的中点
的中点![]() ,如图所示,以
,如图所示,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,
,
则![]() .
.
![]() .
.
设![]() 为平面
为平面![]() 的法向量.
的法向量.
则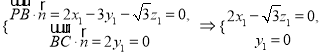
取![]() ,则
,则![]() .
.
易证![]() 平面
平面![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
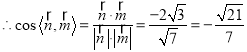 ,
,
由图可知,二面角![]() 为钝角.
为钝角.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018届高三·湖南十校联考)已知函数f(x)=x+sin x(x∈R),且f(y2-2y+3)+f(x2-4x+1)≤0,则当y≥1时, ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. [1,3![]() -3] D.
-3] D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的焦点为
的焦点为![]() ,过抛物线
,过抛物线![]() 上的动点
上的动点![]() (除顶点
(除顶点![]() 外)作
外)作![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() .过点
.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() (垂足为
(垂足为![]() )与直线
)与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x),且对任意x>0,都有f′(x)>![]() .
.
(1)判断函数F(x)=![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(3)请将(2)中结论推广到一般形式,并证明你所推广的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com