
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 以
以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,设点
轴正半轴为极轴建立极坐标系,设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为正三角形.
为正三角形.
(1)求点![]() ,
,![]() 的极坐标;
的极坐标;
(2)若点![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
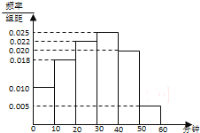
(1)若日均收看该体育节目时间在![]() 内的观众中恰有两名女性,现日均收看时间在
内的观众中恰有两名女性,现日均收看时间在![]() 内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错误概率不超过
人,完成答题卡中的列联表并判断能否在犯错误概率不超过![]() 的前提下认为体育迷与性别有关系?
的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |
附表及公式: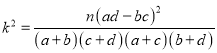 ,
,![]()
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,我国在电动汽车领域有了长足的发展,电动汽车的核心技术是动力总成,而动力总成的核心技术是电机和控制器,我国永磁电机的技术已处于国际领先水平.某公司计划今年年初用196万元引进一条永磁电机生产线,第一年需要安装、人工等费用24万元,从第二年起,包括人工、维修等费用每年所需费用比上一年增加8万元,该生产线每年年产值保持在100万元.
(1)引进该生产线几年后总盈利最大,最大是多少万元?
(2)引进该生产线几年后平均盈利最多,最多是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为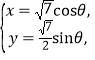 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :不等式
:不等式![]() 对一切正实数
对一切正实数![]() 均成立.
均成立.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
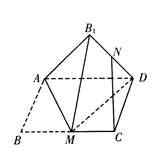
A.存在某个位置,使得![]() B.翻折过程中,
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]() ;D.若
;D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com