
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,在
,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)中求的是在x=1的切线方程,所以直接出函数在x=1的导数,和切点即可解决。(2)求单调性区间,先注意定义域,再求导数等于0的根,一般对于含参的问题,我们先看是否能因式分解。(3)存在![]() 成立,先变形为
成立,先变形为![]() ,从而构造函数
,从而构造函数![]() 在
在![]() 上的最小值
上的最小值![]() .同时注意第(2)问己求对本问的应用。
.同时注意第(2)问己求对本问的应用。
试题解析:
(1)当![]() 时,
时, ![]() ,切点
,切点![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() .
.
(2)![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
①当![]() ,即
,即![]() 时,令
时,令![]() ,因为
,因为![]() ,所以
,所以![]() .
.
令![]() ,因为
,因为![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() ,令
,令![]() 恒成立,
恒成立,
综上,当![]() 时,
时, ![]() 唉
唉![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
(3)由题意可知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
即在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,
即函数![]() 在
在![]() 上的最小值
上的最小值![]() .
.
由第(2)问,
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ;
;
③当![]() ,即
,即![]() 时,
时, ![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
此时不存在![]() 使得
使得![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
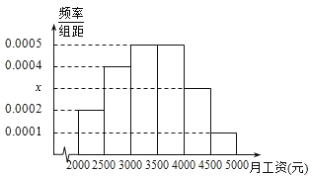
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若双曲线![]() 的右焦点即为曲线
的右焦点即为曲线![]() 的右顶点,直线
的右顶点,直线![]() 为
为![]() 的一条渐近线.
的一条渐近线.
①.求双曲线C的方程;
②.过点![]() 的直线
的直线![]() ,交双曲线
,交双曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点(
点(![]() 点与
点与![]() 的顶点不重合),当
的顶点不重合),当![]() ,且
,且![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
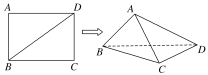
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 的两条对角线
的两条对角线![]() 相交于
相交于![]() ,现用五种颜色(其中一种为红色)对图中四个三角形
,现用五种颜色(其中一种为红色)对图中四个三角形![]() 进行染色,且每个三角形用一种颜色图染.
进行染色,且每个三角形用一种颜色图染.
(1)若必须使用红色,求四个三角形![]() 中有且只有一组相邻三角形同色的染色方法的种数;
中有且只有一组相邻三角形同色的染色方法的种数;
(2)若不使用红色,求四个三角形![]() 中所有相邻三角形都不同色的染色方法的种数.
中所有相邻三角形都不同色的染色方法的种数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
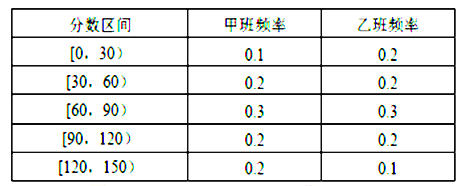
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
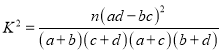 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com