Question

2．在△ABC中，设$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，且|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}•\overrightarrow{b}$=$-\sqrt{3}$，则AB的长为（　　）

• A． $\sqrt{7+2\sqrt{3}}$
• B． $\sqrt{7-2\sqrt{3}}$
• C． $\sqrt{7-\sqrt{3}}$
• D． 7-2$\sqrt{3}$

Answer 1

分析 根据条件可以得到$cos＜\overrightarrow{a}，\overrightarrow{b}＞=-\frac{1}{2}$，即得到$cosC=-\frac{1}{2}$，这样在△ABC中，$AC=\sqrt{3}，BC=2$，从而根据余弦定理即可求出AB的长．

解答 解：如图，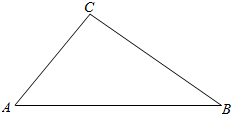

$|\overrightarrow{a}|=2，|\overrightarrow{b}|=\sqrt{3}，\overrightarrow{a}•\overrightarrow{b}=-\sqrt{3}$；
∴$2•\sqrt{3}•cos＜\overrightarrow{a}，\overrightarrow{b}＞=-\sqrt{3}$；
∴$cos＜\overrightarrow{a}，\overrightarrow{b}＞=-\frac{1}{2}$；
即cos$C=-\frac{1}{2}$；
∴由余弦定理得，$A{B}^{2}=4+3-2•2•\sqrt{3}•（-\frac{1}{2}）=7+2\sqrt{3}$；
∴$AB=\sqrt{7+2\sqrt{3}}$．
故选：A．

点评 考查向量数量积的计算公式，向量夹角的概念，以及余弦定理．