
分析 (1)设乙、丙各自回答对的概率分别是p1,p2,由已知条件利用对立事件概率计算公式和相互独立事件乘法概率公式能求出乙、丙两人各自回答对这道题目的概率.
(2)由已知得ξ可能取值0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(1)设乙、丙各自回答对的概率分别是p1,p2,
根据题意,得$\left\{\begin{array}{l}{(1-\frac{3}{4})•(1-{p}_{2})=\frac{1}{12}}\\{{p}_{1}•{p}_{2}=\frac{1}{4}}\end{array}\right.$,
解得${p}_{1}=\frac{3}{8}$,p2=$\frac{2}{3}$.…(5分)
(2)由已知得ξ可能取值0,1,2,3,
P(ξ=0)=$\frac{1}{4}×\frac{5}{8}×\frac{1}{3}=\frac{5}{96}$,
P( ξ=1)=$\frac{3×5×1+1×3×1+1×5×2}{96}$=$\frac{28}{96}$=$\frac{7}{24}$,
P(ξ=2)=$\frac{3×3×1+3×5×2+1×3×2}{96}$=$\frac{45}{96}$=$\frac{15}{32}$,
P(ξ=3)=$\frac{3×3×2}{96}$=$\frac{18}{96}$=$\frac{3}{16}$.…(8分)
∴ξ的分布列如下:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{5}{96}$ | $\frac{7}{24}$ | $\frac{15}{32}$ | $\frac{3}{16}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式和相互独立事件乘法概率公式的灵活运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{9}$ | B. | $\frac{21}{25}$ | C. | $\frac{61}{16}$ | D. | $\frac{126}{275}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.0009 | B. | 0.001 | C. | 0.009 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
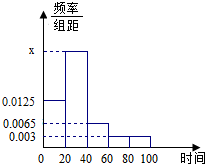 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
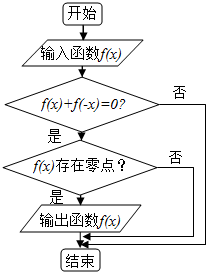 某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )
某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )| A. | f(x)=x2 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=ex | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com