
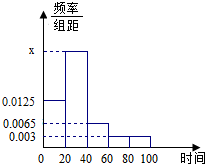
 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].分析 (1)由频率分布直方图中各小矩形面积之和为1,能求出直方图中x的值.
(2)先求出新生上学所需时间不少于60分钟的频率,由此能求出1000名新生中有多少名学生可以申请住宿.
(3)由题设知X的可能取值为0,1,2,分别求出其概率,由此能求出X的分布列和数学期望.
解答 解:(1)由直方图可得:
20×x+0.0125×20+0.0065×20+0.003×2×20=1.
所以 x=0.025.…(2分)
(2)新生上学所需时间不少于60分钟的频率为:
0.003×2×20=0.12…(4分)
因为1000×0.12=120
所以1000名新生中有120名学生可以申请住宿.…(6分)
(3)由题设知X的可能取值为0,1,2.…(7分)
P(X=0)=$\frac{{C}_{2}^{0}{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$,P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,P(X=2)=$\frac{{C}_{2}^{2}{C}_{4}^{0}}{{C}_{6}^{2}}$=$\frac{1}{15}$,
所以X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望,是中档题,读懂频率分布直方图的数据含义是关键.


科目:高中数学 来源: 题型:选择题
| A. | log34=$\frac{lg4}{lg3}$ | B. | log34=$\frac{ln4}{ln3}$ | ||
| C. | log34=$\frac{1}{lo{g}_{4}3}$ | D. | log34=$\frac{lo{g}_{1}4}{lo{g}_{1}3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com