

分析 (1)由频率公式和图求出样本容量n,由频率分布直方图中的数据求出x、y的值;
(2)先求出分数在[80,90)、[90,100]内的学生人数,求出抽取的3名学生中得分在[80,90)的人数X的可能取值,由概率公式分别求出它们的概率并列出X的分布列,代入公式求出EX.
解答 解:(1)由题意可知,样本容量n=$\frac{8}{0.016×10}$=50,y=$\frac{2}{50×10}$=0.004,
x=0.100-0.004-0.010-0.016-0.040=0.030.…(4分)
(2)由题意可知,分数在[80,90)内的学生有5人,分数在[90,100]内的学生有2人,共7人.
抽取的3名学生中得分在[80,90)的人数X的可能取值为1,2,3,则
P(X=1)=$\frac{{C}_{5}^{1}{C}_{2}^{2}}{{C}_{7}^{3}}$=$\frac{1}{7}$,P(X=2)=$\frac{{C}_{5}^{2}{C}_{2}^{1}}{{C}_{7}^{3}}$=$\frac{4}{7}$,P(X=3)=$\frac{{C}_{5}^{3}{C}_{2}^{0}}{{C}_{7}^{3}}$=$\frac{2}{7}$.
所以X的分布列为
| X | 1 | 2 | 3 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
点评 本题考查茎叶图、频率分布直方图,随机变量X的分布列及数学期望,以及古典概型,比较综合.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
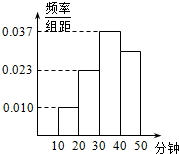 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )| A. | 180 | B. | 450 | C. | 360 | D. | 270 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com