
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
分析 求出出现2次正面一次反面的概率,再加上3次都是正面的概率,即为所求.
解答 解:将一枚均匀的硬币投掷3次,出现2次正面一次反面的概率等于${C}_{3}^{2}$•${(\frac{1}{2})}^{2}$•$\frac{1}{2}$=$\frac{3}{8}$,
三次都是正面的概率等于(${(\frac{1}{2})}^{3}$=$\frac{1}{8}$,
∴掷一枚均匀的硬币3次,出现正面的次数多于反面的次数的概率是$\frac{3}{8}$+$\frac{1}{8}$=$\frac{1}{2}$,
故选:A.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键,属于基础题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.0009 | B. | 0.001 | C. | 0.009 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
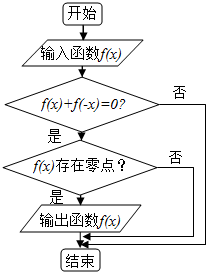 某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )
某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )| A. | f(x)=x2 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=ex | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
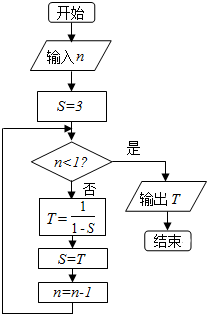
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com