
【题目】已知正三棱柱ABC﹣A1B1C1的各个棱长都相等,E为BC的中点,动点F在CC1上,且不与点C重合
(1)当CC1=4CF时,求证:EF⊥A1C
(2)设二面角C﹣AF﹣E的大小为α,求tanα的最小值.
【答案】
(1)证明:过E作EN⊥AC于N,连接EF,NF,AC1,
由直棱柱的性质可知,底面ABC⊥侧面A1C,
∴EN⊥侧面A1C,NF为EF在侧面A1C内的射影,
设正三棱柱ABC﹣A1B1C1的各个棱长为4,
∵CC1=4CF,∴在直角三角形CNF中,CN=1,
则由 ![]() =
= ![]() =
= ![]() ,得NF∥AC1,
,得NF∥AC1,
又AC1⊥A1C,故NF⊥A1C,
由三垂线定理可知EF⊥A1C
(2)解:连接AF,过N作NM⊥AF于M,连接ME
由(I)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=α,
设∠FAC=θ,则0°<θ≤45°,
在直角三角形CNE中,NE= ![]() ,
,
在直角三角形AMN中,MN=3sinθ
故tanα= ![]() ,又0°<θ≤45°,∴0<sinθ≤
,又0°<θ≤45°,∴0<sinθ≤ ![]()
故当θ=45°时,tanα达到最小值,
∴tanα的最小值为anα= ![]() .
.
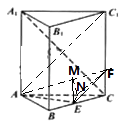
【解析】(1)过E作EN⊥AC于N,连接EF,NF,AC1 , 则EN⊥侧面A1C,NF为EF在侧面A1C内的射影,设正三棱柱ABC﹣A1B1C1的各个棱长为4,则CN=1,NF∥AC1 , 推导出C1⊥A1C,NF⊥A1C,由此能证明EF⊥A1C.(2)连接AF,过N作NM⊥AF于M,连接ME,则EN⊥侧面A1C,根据三垂线定理得EM⊥AF,∠EMN是二面角C﹣AF﹣E的平面角由此能示出tanα的最小值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图: 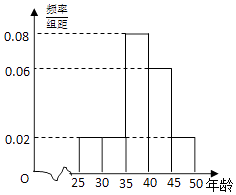
(1)如表是年龄的频数分布表,求a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)根据频率分布直方图估计志愿者年龄的平均数和中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)当x∈[0, ![]() ]时,求|
]时,求| ![]() +
+ ![]() |的取值范围;
|的取值范围;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求当k为何值时,g(x)的最小值为﹣
,求当k为何值时,g(x)的最小值为﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() 、
、 ![]() 满足|
满足| ![]() |=1,|
|=1,| ![]() |=2,
|=2, ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
(1)若(k ![]() ﹣
﹣ ![]() )⊥(
)⊥( ![]() +
+ ![]() ),求k的值;
),求k的值;
(2)若|k ![]() ﹣
﹣ ![]() |<2,求k的取值范围.
|<2,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. (Ⅰ)求直方图中a的值;
(Ⅱ)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(Ⅲ)若该市政府希望使80%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣2cosx),
=(sinx,﹣2cosx), ![]() =(sinx+
=(sinx+ ![]() cosx,﹣cosx),x∈R.函数f(x)=
cosx,﹣cosx),x∈R.函数f(x)= ![]()
![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题: 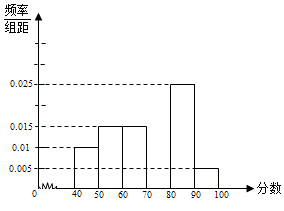
(Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com