
 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.分析 (1)取AB1的中点E,AB的中点F.连接DE、EF、CF.证明DE的平行线CF垂直平面ABB1A1,内的相交直线AB,BB1,即可证明平面AB1D⊥平面ABB1A1;
(2)建立空间直角坐标系,求平面AB1D的一个法向量,以及平面ABC的一个法向量,利用向量的数量积求平面AB1D与平面ABC所成二面角(锐角)的大小.
解答 证明:(1)取AB1的中点E,AB的中点F.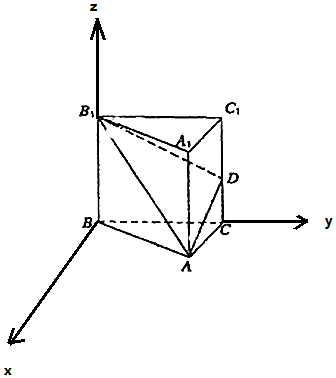
连接DE、EF、CF.
∵直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点,
∴EF$\underset{∥}{=}$$\frac{1}{2}$BB1,CD$\underset{∥}{=}$$\frac{1}{2}$BB1.
∴四边形CDEF为平行四边形,∴DE∥CF.
又三棱柱ABC-A1B1C1是直三棱柱.
△ABC为正三角形.CF?平面ABC,
∴CF⊥BB1,CF⊥AB,而AB∩BB1=B,∴CF⊥平面ABB1A1,
又DE∥CF,∴DE⊥平面ABB1A1.
又DE?平面AB1D.所以平面AB1D⊥平面ABB1A1.
解:(2)建立如图所示的空间直角坐标系,
则A($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$,0),C(0,a,0),D(0,a,$\frac{a}{2}$)B1(0,0,a),B(0,0,0),
$\overrightarrow{A{B}_{1}}$=(-$\frac{\sqrt{3}a}{2}$,-$\frac{a}{2}$,a),$\overrightarrow{AD}$=(-$\frac{\sqrt{3}a}{2},\frac{a}{2},\frac{a}{2}$),
设$\overrightarrow{n}$=(1,x,y)为平面AB1D的一个法向量.
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=-\frac{\sqrt{3}a}{2}-\frac{ax}{2}+ay=0}\\{\overrightarrow{n}•\overrightarrow{AD}=-\frac{\sqrt{3}a}{2}+\frac{ax}{2}+\frac{ay}{2}=0}\end{array}\right.$,解得$\overrightarrow{n}$=(1,$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),
平面ABC的一个法向量为$\overrightarrow{m}$=(0,0,1).
设平面AB1D与平面ABC所成二面角(锐角)为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\frac{2\sqrt{3}}{3}}{\sqrt{\frac{8}{3}}}$=$\frac{\sqrt{2}}{2}$,
∴θ=$\frac{π}{4}$.
∴平面AB1D与平面ABC所成二面角(锐角)的大小为$\frac{π}{4}$.
点评 本题考查平面与平面垂直的判定,二面角及其度量,考查空间想象能力,计算能力,是中档题.证明平面与平面垂直主要转化为证明一个平面内的一条直线与另一个平面垂直即可,而证明直线与平面垂直,只需证明此直线与平面图内的两条相交直线垂直;求二面角的大小新教材主要要求学生掌握用空间向量的方法来求:第一步建立适当的空间直角坐标系,并设出点的坐标;第二步分别求出二面角的两个面的一个法向量;第三步代公式$cos\left?{\overrightarrow m,\overrightarrow n}\right>=\frac{|\overrightarrow m•\overrightarrow n|}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}$即可求得,注意运算的准确性.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 15 | C. | 32 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 很小的实数可以构成集合 | |
| B. | 自然数集N中最小的数是1 | |
| C. | 集合{y|y=x2-1}与{(x,y)|y=x2-1}是同一个集合 | |
| D. | 空集是任何集合的子集 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
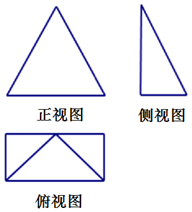 一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.
一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 10+10$\sqrt{2}$ | C. | 20 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 计算小于100的奇数的连乘积 | |
| B. | 计算从1开始的连续奇数的连乘积 | |
| C. | 从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数 | |
| D. | 计算1×3×5×…×n≥100时的最小的n值. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com