
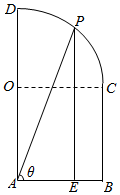
 已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.
已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.分析 (Ⅰ)连接OP,由P为$\widehat{CD}$的中点,得出∠POC=45°,利用三角函数求出AE与PE的值,即可得出△APE的面积;
(Ⅱ)由∠PAB=θ,得出∠POD=∠APO=∠APE=$\frac{π}{2}$-θ,求出,利用三角函数求出AE与PE的值,即可得出y的解析式,
再根据θ的取值范围求出f(θ)的值域.
解答 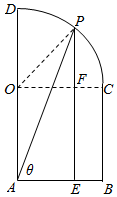 解:(Ⅰ)连接OP,如图所示:
解:(Ⅰ)连接OP,如图所示:
∵P为$\widehat{CD}$的中点,
∴PF=OP•sin45°=$\frac{\sqrt{2}}{2}$,
OF=OP•cos45°=$\frac{\sqrt{2}}{2}$,
∴△APE的面积S=$\frac{1}{2}$AE•PE=$\frac{1}{2}$•OF•(PF+FE)=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×($\frac{\sqrt{2}}{2}$+1)=$\frac{1+\sqrt{2}}{4}$;
(Ⅱ)当点P在$\widehat{CD}$上运动时,设∠PAB=θ,则θ∈[$\frac{π}{4}$,$\frac{π}{2}$];
∴∠POD=$\frac{π}{2}$-θ,
∴∠APO=∠APE=$\frac{π}{2}$-θ,
∴∠POC=$\frac{π}{2}$-2($\frac{π}{2}$-θ)=2θ-$\frac{π}{2}$,
∴PF=OP•sin(2θ-$\frac{π}{2}$)=-cos2θ,
∴PE=PF+FE=-cos2θ+1,
AE=OP•cos(2θ-$\frac{π}{2}$)=sin2θ,
∴y=AE+PE=sin2θ+(-cos2θ+1)=$\sqrt{2}$sin(2θ-$\frac{π}{4}$)+1,
即y=f(θ)=$\sqrt{2}$sin(2θ-$\frac{π}{4}$)+1,θ∈[$\frac{π}{4}$,$\frac{π}{2}$];
∴2θ-$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{3π}{4}$],
∴sin(2θ-$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2}$,1],
∴$\sqrt{2}$sin(2θ-$\frac{π}{4}$)+1∈[2,$\sqrt{2}$+1],
即f(θ)的值域是[2,$\sqrt{2}$+1].
点评 本题考查了三角函数的化简与计算问题,也考查了三角函数的图象与性质的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意x∈R,|x|<0 | B. | 任意x∈R,|x|≤0 | C. | 彐x∈R,|x|<0 | D. | 彐x∈R,|x|≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com