
分析 直接由已知结合等差数列的性质与前n项和得S15>0,S16<0,则答案可求,
由题意可知,该数列是递减数列,当n=8时,|a8|最小,且|S8|最大,问题得以解决.
解答 解:∵等差数列{an}满足a8>0,a8+a9<0,
∴S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=15a8>0,
S16=$\frac{16}{2}$(a1+a16)=8(a8+a9)<0,
∴Sn>0的最大n是15,
∵等差数列{an}的前n项和为Sn,且满足a8>0,a8+a9<0,
∴该数列是递减数列,当n=8时,|a8|最小,且|S8|最大,
∴数列{$\frac{{S}_{n}}{{a}_{n}}$}(1≤n≤15)中最大的项为第8项
故答案为15,8.
点评 本题考查了等差数列的性质,考查了等差数列的前n项和,是基础题.


科目:高中数学 来源: 题型:解答题
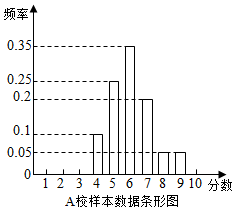 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
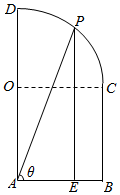 已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.
已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com