
 ij����֯��һȫ��ѧ���μӼ���������������ȼ���Ϊ1��10�֣����������A��B����ѧУ��60��ѧ���ijɼ����õ��������������
ij����֯��һȫ��ѧ���μӼ���������������ȼ���Ϊ1��10�֣����������A��B����ѧУ��60��ѧ���ijɼ����õ��������������| �ɼ����֣� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ���������� | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
���� ���ֱ����AУ������ƽ���ɼ��������BУ������ƽ���ɼ�������Ӷ��õ���Уѧ���ļ�����ɼ�ƽ������ͬ��AУѧ���ļ�����ɼ��Ƚ��ȶ�������÷�����Ƚϼ��У�
������CA1��ʾ�¼���AУѧ��������ɼ�Ϊ8�ֻ�9�֡���CA2��ʾ�¼���AУѧ��������ɼ�Ϊ9�֡���CB1��ʾ�¼���BУѧ��������ɼ�Ϊ7�֡���CB2��ʾ�¼���BУѧ��������ɼ�Ϊ8�֡�����CA1��CB1������CA2��CB2������CB1��CB2���⣬C=CB1CA1��CB2CA2���ɴ������P��C����
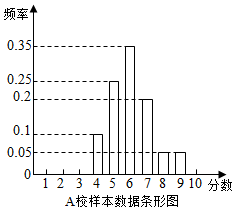
��� �⣺����AУ�������ݵ�����ͼ֪��
�ɼ��ֱ�Ϊ4�֡�5�֡�6�֡�7�֡�8�֡�9�ֵ�ѧ���ֱ��У�
6�ˡ�15�ˡ�21�ˡ�12�ˡ�3�ˡ�3�ˣ�
AУ������ƽ���ɼ�Ϊ��$\overline{{x}_{A}}$=$\frac{4��6+5��15+6��21+7��12+8��3+9��3}{60}$=6���֣���
AУ�����ķ���Ϊ${{S}_{A}}^{2}$=$\frac{1}{60}$[6��4-6��2+15��5-6��2+21��6-6��2+12��7-6��2+3��8-6��2+3��9-6��2]=1.5��
��BУ��������ͳ�Ʊ�֪��
BУ������ƽ���ɼ�Ϊ��$\overline{{x}_{B}}$=$\frac{4��9+5��12+6��21+7��9+8��6+9��3}{60}$=6���֣���
BУ�����ķ���Ϊ${{S}_{B}}^{2}$=$\frac{1}{60}$[9��4-6��2+12��5-6��2+21��6-6��2+9��7-6��2+6��8-6��2+3��9-6��2]=1.8��
��$\overline{{x}_{A}}$=$\overline{{x}_{B}}$��${{S}_{A}}^{2}��{{S}_{B}}^{2}$��
����Уѧ���ļ�����ɼ�ƽ������ͬ��AУѧ���ļ�����ɼ��Ƚ��ȶ�������÷�����Ƚϼ��У�
������CA1��ʾ�¼���AУѧ��������ɼ�Ϊ8�ֻ�9�֡���CA2��ʾ�¼���AУѧ��������ɼ�Ϊ9�֡���
CB1��ʾ�¼���BУѧ��������ɼ�Ϊ7�֡���CB2��ʾ�¼���BУѧ��������ɼ�Ϊ8�֡���
��CA1��CB1������CA2��CB2������CB1��CB2���⣬C=CB1CA1��CB2CA2��
P��C��=P��CB1CA1��CB2CA2��=P��CB1CA1��+P��CB2CA2��
=P��CB1��P��CA1��+P��CB2��P��CA2����
���������ݵ�P��CA1��=$\frac{6}{60}$��P��CA2��=$\frac{3}{60}$��P��CB1��=$\frac{9}{60}$��P��CB2��=$\frac{6}{60}$��
��P��C��=$\frac{9}{60}��\frac{6}{60}+\frac{6}{60}��\frac{3}{60}=0.02$��
���� ���⿼��ƽ�������������Ӧ�ã�������ʵ������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��1��2�� | C�� | ��2��4�� | D�� | ��0��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{3}$ | B�� | $\frac{2\sqrt{15}}{3}$ | C�� | $\frac{3\sqrt{5}}{4}$ | D�� | $\frac{\sqrt{15}}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -1 | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com