
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{15}}{3}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{\sqrt{15}}{6}$ |
分析 可作出图形,根据题意可知λ,μ>0,根据条件对$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$两边平方,进行数量积的运算便可得到5=4λ2+2λμ+μ2=(2λ+μ)2-2λμ,由基本不等式即可得出2λ+μ的范围,从而便可得出2λ+μ的最大值.
解答  解:如图,依题意知,λ>0,μ>0;
解:如图,依题意知,λ>0,μ>0;
根据条件,
5=${\overrightarrow{AP}}^{2}={λ}^{2}{\overrightarrow{AB}}^{2}+2λμ\overrightarrow{AB}•\overrightarrow{AD}+{μ}^{2}{\overrightarrow{AD}}^{2}$
=4λ2+2λμ+μ2
=$(2λ+μ)^{2}-2λμ≥(2λ+μ)^{2}-(\frac{2λ+μ}{2})^{2}$=$\frac{3}{4}(2λ+μ)^{2}$;
∴$(2λ+μ)^{2}≤\frac{20}{3}$;
∴$2λ+μ≤\frac{2\sqrt{15}}{3}$;
∴2λ+μ的最大值为$\frac{2\sqrt{15}}{3}$.
故选B.
点评 考查向量数量积的运算及计算公式,以及配方法的应用,基本不等式的应用,一元二次不等式的解法.


科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0≤x≤1} | C. | {x|x≤1} | D. | {x|x≥0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
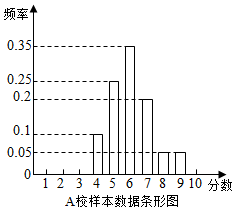 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com