
| A. | 2 | B. | -1 | C. | 0 | D. | 1 |
分析 由已知得随机变量ξ的所有可能取值为0,1,且P(ξ=1)=p,P(ξ=0)=1-p,推导出 E(ξ)=p,D(ξ)=p-p2,从而得到$\frac{4Dξ-1}{Eξ}$=4-(4p+$\frac{1}{p}$),由此利用均值定理能求出$\frac{4Dξ-1}{Eξ}$的最大值.
解答 解:随机变量ξ的所有可能取值为0,1,
并且有P(ξ=1)=p,P(ξ=0)=1-p,
从而 E(ξ)=0×(1-p)+1×p=p,
D(ξ)=(0-p)2×(1-p)+(1-p)2×p=p-p2,
$\frac{4Dξ-1}{Eξ}$=$\frac{4(p-{p}^{2})-1}{p}$=4-(4p+$\frac{1}{p}$),
∵0<p<1,
∴4p+$\frac{1}{p}$$≥2\sqrt{4p×\frac{1}{p}}$=4,
当4p=$\frac{1}{p}$,p=$\frac{1}{2}$时,取“=”,
∴当p=$\frac{1}{2}$时,
$\frac{4Dξ-1}{Eξ}$取得最大值0.
故选:C.
点评 本题考查关于数学期望和方差的代数式的取大值的求法,是中档题,解题时要认真审题,注意离散型随机变量的数学期望与方差的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
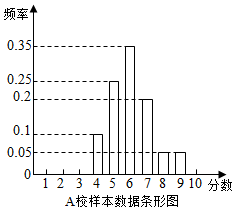 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 2 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com