
分析 (1)利用数列递推关系、等差数列的通项公式即可得出.
(2)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)∵${S_n}={n^2}+c$,
∴a1=S1=1+c,a2=S2-S1=(4+c)-(1+c)=3,a3=S3-S2=5…(2分)
又∵{an}等差数列,∴6+c=6,c=0; …(3分)
d=3-1=2;a1=S1=1+c=1,…(4分)
∴an=1+2(n-1)=2n-1…(5分)
(2)${b_n}=\frac{2n-1}{2^n}$…(6分)
${T_n}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-3}{{{2^{n-1}}}}+\frac{2n-1}{2^n}$…①…(7分)
$\frac{1}{2}{T_n}=\begin{array}{l}{\;}&{\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+…+\frac{2n-3}{2^n}+\frac{2n-1}{{{2^{n+1}}}}}\end{array}$…②…(8分)
①-②得 $\frac{1}{2}{T_n}=\frac{1}{2}+2(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{2^n})-\frac{2n-1}{{{2^{n+1}}}}$…(9分)
$\frac{1}{2}{T_n}=\frac{1}{2}+2×\frac{{\frac{1}{2^2}[1-{{(\frac{1}{2})}^{n-1}}]}}{{1-\frac{1}{2}}}-\frac{2n-1}{{{2^{n+1}}}}$…(10分)
$\frac{1}{2}{T_n}=\frac{3}{2}-\frac{2n+3}{{{2^{n+1}}}}$…1(1分)
${T_n}=3-\frac{2n+3}{2^n}$…(12分)
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{15}$ | B. | $\frac{13}{15}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
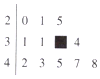 在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
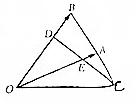 在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.
在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com