
| A. | ?x0∈R,使得e${\;}^{{x}_{0}}$≤0 | B. | $sinx+\frac{2}{sinx}≥2\sqrt{2}(x≠kπ,k∈Z)$ | ||
| C. | ?x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分不必要条件 |
分析 根据指数函数性质即可判断A错误;通过举反例可判断选项B、C均错误;若a>1,b>1,则ab>1显然成立,反之不成立,故选项D正确.
解答 解:对于选项A:根据指数函数性质,?x∈R,ex>0,故A错误;
对于选项B:当x=$-\frac{π}{2}$时,$sinx+\frac{2}{sinx}$=-3,故B错误;
对于选项C:当x=-1时,${2}^{x}=\frac{1}{2},{x}^{2}=1$,此时2x<x2,故C错误;
对于选项D:若a>1,b>1,则ab>1显然成立;反之不成立,例如a=4,b=$\frac{1}{2}$.所以a>1,b>1是ab>1的充分不必要条件,故D正确.
故选:D
点评 本题通过判断命题的真假考查了基本初等函数的性质,三角函数以及不等式等知识点,属于基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (-∞,3)∪(4,+∞) | C. | (4,+∞) | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
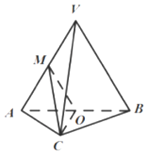 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,三角形VAB为等边三角形,AC⊥BC且 AC=BC=$\sqrt{2}$,O、M分别为AB和VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,三角形VAB为等边三角形,AC⊥BC且 AC=BC=$\sqrt{2}$,O、M分别为AB和VA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,6) | B. | (3,-6) | C. | (-6,3) | D. | (6,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com