
分析 (1)设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得:c=$\sqrt{3}$,$\frac{3}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1,a2=b2+c2,联立解出即可得出.
(2)由题意可知:直线l的斜率不为零,设直线l方程:x-my-n=0与圆O:x2+y2=1相切,可得$\frac{|n|}{\sqrt{1+{m}^{2}}}$=1.设A(x1,y1),B(x2,y2),直线方程与椭圆方程联立可得:(m2+4)y2+2mny+n2-4=0,可得:|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|,S△AOB=$\frac{1}{2}$d|AB|,λ=$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2,由$\frac{1}{2}$≤λ≤$\frac{2}{3}$,令t=m2+1,则λ=$\frac{t}{t+3}$,可得t∈[3,6],利用基本不等式的性质即可得出.
解答 解:(1)设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得:c=$\sqrt{3}$,$\frac{3}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1,a2=b2+c2,
联立解得:a=2,b=1.
∴椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}}$+y2=1.
(2)由题意可知:直线l的斜率不为零,
设直线l方程:x-my-n=0与圆O:x2+y2=1相切,
∴$\frac{|n|}{\sqrt{1+{m}^{2}}}$=1,解得n2=m2+1.
设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{x=my+n}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$,
消去x整理得:(m2+4)y2+2mny+n2-4=0,
∴y1+y2=-$\frac{2mn}{{m}^{2}+4}$,y1y2=$\frac{{n}^{2}-4}{{m}^{2}+4}$.
又∵|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|,
∴${S_{△AOB}}=\frac{1}{2}d•|{AB}|=\frac{1}{2}•\frac{|n|}{{\sqrt{1+{m^2}}}}•\sqrt{1+{m^2}}•|{{y_1}-{y_2}}|$=$\frac{1}{2}|n|•|{{y_1}-{y_2}}|=2\sqrt{3}•\sqrt{\frac{n^2}{{{{({{m^2}+4})}^2}}}}=2\sqrt{3}•\sqrt{\frac{{{m^2}+1}}{{{{({{m^2}+4})}^2}}}}$,
λ=$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2=$\frac{5{n}^{2}-4{m}^{2}-4}{{m}^{2}+4}$=$\frac{{m}^{2}+1}{{m}^{2}+4}$,
∵$\frac{1}{2}$≤λ≤$\frac{2}{3}$,令t=m2+1,
则λ=$\frac{t}{t+3}$,可得t∈[3,6],
∴S△AOB=2$\sqrt{3}$$\sqrt{\frac{t}{(t+3)^{2}}}$=$\frac{2\sqrt{3}}{\sqrt{t+\frac{9}{t}+6}}$,
∵$t+\frac{9}{t}$∈$[6,\frac{15}{2}]$,∴($t+\frac{9}{t}$+6)∈$[12,\frac{27}{2}]$,
∴$\sqrt{t+\frac{9}{t}+6}$∈$[\sqrt{12},\sqrt{\frac{27}{2}}]$,
∴S△AOB∈$[\frac{2\sqrt{2}}{3},1]$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质、三角形面积计算公式、基本不等式的性质、弦长公式,考查了推理能力与计算能力,属于难题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{5}$ | B. | 3 | C. | $\frac{16}{5}$ | D. | $\frac{18}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得e${\;}^{{x}_{0}}$≤0 | B. | $sinx+\frac{2}{sinx}≥2\sqrt{2}(x≠kπ,k∈Z)$ | ||
| C. | ?x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1,y=$\frac{x}{x}$ | B. | y=lgx2,y=2lgx | C. | y=x,y=$\root{5}{{x}^{5}}$ | D. | y=|x|,y=($\sqrt{x}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
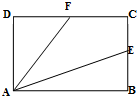
| A. | 2.5 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com