
| A. | (-3,6) | B. | (3,-6) | C. | (-6,3) | D. | (6,-3) |
分析 根据题意设出$\overrightarrow{b}$=(-2x,x),x>0,利用模长公式列出方程求出x的值.
解答 解:由平面向量$\overrightarrow b$与向量$\overrightarrow a=(2,-1)$的夹角是180°,
设$\overrightarrow{b}$=(-2x,x),x>0;
由$|\overrightarrow b|=3\sqrt{5}$,
得(-2x)2+x2=${(3\sqrt{5})}^{2}$,
解得x=3;
所以$\overrightarrow b$=(-6,3).
故选:C.
点评 本题考查了利用平面向量的模长公式与应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得e${\;}^{{x}_{0}}$≤0 | B. | $sinx+\frac{2}{sinx}≥2\sqrt{2}(x≠kπ,k∈Z)$ | ||
| C. | ?x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9π | B. | 324π | C. | 81π | D. | $\frac{243}{2}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
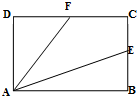
| A. | 2.5 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{{\begin{array}{l}{3-{x^2}(x>0)}\\{2(x=0)}\\{1-2x(x<0)}\end{array}}$,
已知函数f(x)=$\left\{{\begin{array}{l}{3-{x^2}(x>0)}\\{2(x=0)}\\{1-2x(x<0)}\end{array}}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com