
分析 四边形ABCD是空间四边形,而不是平面四边形,要想求MN与AC,BD的关系,必须将它们转化到平面来考虑.取AD的中点为G,再连接MG,NG,利用三角形三边间的相互关系能求出结果.
解答 解:四边形ABCD是空间四边形,而不是平面四边形,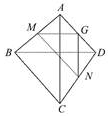
要想求MN与AC,BD的关系,必须将它们转化到平面来考虑.
取AD的中点为G,再连接MG,NG,
在△ABD中,M,G分别是线段AB,AD的中点,
则MG∥BD,且MG=$\frac{1}{2}$BD,
同理,在△ADC中,NG∥AC,且NG=$\frac{1}{2}$AC,
又根据三角形的三边关系知,MN<MG+NG,
即MN<$\frac{1}{2}$BD+$\frac{1}{2}$AC=$\frac{1}{2}$(AC+BD).
∴MN<(AC+BD).
故答案为:<.
点评 本题考查线段长与两线段和的大小的比较,是中档题,解题时要认真审题,注意化空间问题为平面问题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
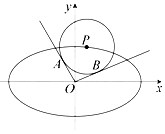 如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{a^2}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$分别相切于A,B两点.
如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{a^2}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$分别相切于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,6] | B. | [-3,3]∪[5,+∞) | C. | $[{-6,4+\sqrt{6}}]$ | D. | $[{-6,6}]∪[{4+\sqrt{6},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {1,2} | C. | {0,3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {0,1} | C. | {0,1,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com