
| A. | $\frac{c^2}{{{a^2}+{b^2}}}$ | B. | $\frac{a^2}{{{c^2}+{b^2}}}$ | C. | $\frac{b^2}{{{a^2}+{c^2}}}$ | D. | $\frac{a}{{{c^2}+{b^2}}}$ |
分析 此题把点A(cosα,sinα)与点B(cosβ,sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点.结合点到直线的距离公式和三角函数中的恒等变换应用进行解答.
解答 解: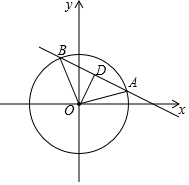 在平面直角坐标系中,点A(cosα,sinα)与点B(cosβ,sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点,如图.
在平面直角坐标系中,点A(cosα,sinα)与点B(cosβ,sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点,如图.
从而:|AB|2=(cosα-cosβ)2+(sinα-sinβ)2=2-2cos(α-β)=
又∵单位圆的圆心到直线l的距离d=$\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$
由平面几何知识知|OA|2-($\frac{1}{2}$|AB|)2=d2,即1-$\frac{2-2cos(α-β)}{4}$=d2=$\frac{{c}^{2}}{{a}^{2}+{b}^{2}}$
∴${cos^2}\frac{α-β}{2}$=$\frac{1}{2}$[1+cos(α-β)]=$\frac{c^2}{{{a^2}+{b^2}}}$.
故选:A.
点评 本题考查了三角函数中的恒等变换应用和三角函数的化简求值.解题时,利用了“数形结合”的数学思想.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $-\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{10}i$ | D. | $-\frac{{\sqrt{10}}}{10}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{11π}{6}$ | C. | $-\frac{π}{6}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 0 | 1 |
| P | 6a2-a | 3-7a |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{3}$ | D. | 1或$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com