
| A. | 既不充分也不必要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 充要条件 |
分析 由题意,可由函数的性质得出f(x)为[-1,0]上是减函数,再由函数的周期性即可得出f(x)为[3,4]上的减函数,由此证明充分性,再由f(x)为[3,4]上的减函数结合周期性即可得出f(x)为[-1,0]上是减函数,再由函数是偶函数即可得出f(x)为[0,1]上的增函数,由此证明必要性,即可得出正确选项
解答 解:∵f(x)是定义在R上的偶函数,
∴若f(x)为[0,1]上的增函数,则f(x)为[-1,0]上是减函数,
又∵f(x)是定义在R上的以2为周期的函数,且[3,4]与[-1,0]相差两个周期,
∴两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立.
若f(x)为[3,4]上的减函数,同样由函数周期性可得出f(x)为[-1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立.
综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件.
故选D.
点评 本题考查充分性与必要性的判断,解题的关键是理解充分性与必要性证明的方向,即由哪个条件到哪个条件的证明是充分性,哪个方向是必要性,初学者易搞不清证明的方向导致表述上出现逻辑错误.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | D. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
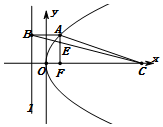 如图,抛物线y2=2px(p>0)的焦点为F,准线为l,过抛物线上一点A作l的垂线,垂足为B,设C($\frac{7}{2}$p,0),AF与BC相交于点E.若|CF|=3|AF|,且△ACE的面积为3,则p的值为2$\sqrt{2}$.
如图,抛物线y2=2px(p>0)的焦点为F,准线为l,过抛物线上一点A作l的垂线,垂足为B,设C($\frac{7}{2}$p,0),AF与BC相交于点E.若|CF|=3|AF|,且△ACE的面积为3,则p的值为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | (-∞,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com