
| A. | 2017 | B. | 2018 | C. | 8068 | D. | 4034 |
分析 由题意对已知函数求两次导数可得f′′(x)=2x-4,由题意可得函数的图象关于点(2,2)对称,即f(x)+f(4-x)=2,由数列{an}的通项公式分析可得{an}为等差数列,且a1+a2017=a2+a2016=…=2a1009=4,而$\sum_{i=1}^{2017}{f({a_i})}$=f(a1)+f(a2)+…+f(a2016)+f(a2017),结合f(x)+f(4-x)=2,计算可得答案.
解答 解:根据题意,三次函数$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$,
则f′(x)=x2-4x+$\frac{8}{3}$,
则f′′(x)=2x-4,
若f′′(x)=2x-4=0,则有x=2,
又由$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$,则f(2)=2,
即(2,2)是三次函数$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$的对称中心,
则有f(x)+f(4-x)=4,
数列{an}的通项公式为an=n-1007,为等差数列,
则有a1+a2017=a2+a2016=…=2a1009=4
则$\sum_{i=1}^{2017}{f({a_i})}$=f(a1)+f(a2)+…+f(a2016)+f(a2017)
=f(a1)+f(a2017)+f(a2)+f(a2016)+…+f(a1008)+f(a1010)+f(a1009)
=4×1008+2=4034;
故选:D.
点评 本题考查函数的值,涉及导数的计算,关键是求出函数f(x)的对称中心.


科目:高中数学 来源: 题型:解答题
| 种植地编号 | A | B | C | D | E |
| (x,y,z) | (1,0,0) | (2,2,1) | (0,1,1) | (2,0,2) | (1,1,1) |
| 种植地编号 | F | G | H | I | J |
| (x,y,z) | (1,1,2) | (2,2,2) | (0,0,1) | (2,2,1) | (0,2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|x-y2|+|x2+y|≤1,则${(x+\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| B. | 若|x-y2|+|x2-y|≤1,则${(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| C. | 若|x+y2|+|x2-y|≤1,则${(x+\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ | |
| D. | 若|x+y2|+|x2+y|≤1,则${(x-\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
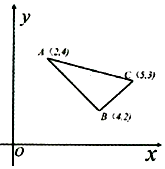 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com