Question

【题目】如图所示，已知四边形是直角梯形，，，其中是上的一点，四边形是菱形，满足，沿将折起，使

（1）求证：平面平面

（2）求三棱锥的体积.

Answer 1

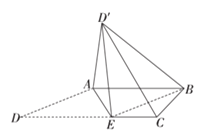
【答案】(1)证明见解析；(2).

【解析】试题分析：

（1）取的中点，取的中点，连接和,和，由题意结合等腰三角形的性质可得，，结合线面垂直的判断定理有面，,而，所以平面，结合面面垂直的判断定理可得平面平面.

（2）由题意结合（1）可知为三棱锥的底面的高，转化顶点计算可得三棱锥的体积.

试题解析：

（1）如图，取的中点，取的中点，连接和,和，由题意知：

，是等腰三角形，

，是等腰三角形，

则有，，

分别为和的中点，可得：,而，，

所以面，可得，,

面，，平面，且与不平行，所以平面，

而平面，所以平面平面.

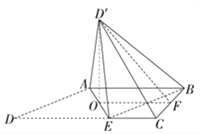
（2）三棱锥的体积，即为三棱锥的体积，由（1）知，平面，从而为三棱锥的底面的高，

为直角三角形，，可得，而，从而，由题意知：，从而，

是等腰三角形，且，为的中点，且，

，

，故.