
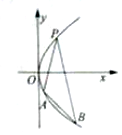
 如图,过抛物线y2=2px(p>0)上一点P(1,2),作两条直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时:
如图,过抛物线y2=2px(p>0)上一点P(1,2),作两条直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时:分析 (1)把点P代入抛物线求得p则抛物线的方程可得,设直线PA的斜率为kPA,直线PB的斜率为kPB,则可分别表示kPA和kPB,根据倾斜角互补可知kPA=-kPB,进而求得y1+y2的值;
(2)表示出面积,利用导数方法求△ABP面积S△ABP的最大值.
解答 解:(1)∵点P(1,2)在抛物线上,∴22=2p,解得p=2.
设直线PA的斜率为kPA,直线PB的斜率为kPB.
则kPA=$\frac{{y}_{1}-2}{{x}_{1}-1}$(x1≠1),kPB=$\frac{{y}_{2}-2}{{x}_{2}-1}$(x2≠1),
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB.
由A(x1,y1),B(x2,y2)均在抛物线上,得
y12=4x1,①y22=4x2,②
∴y1+2=-(y2+2),∴y1+y2=-4.
(2)由①-②得直线AB的斜率为kAB=-1.
因此设直线AB的方程为y=-x+b,由直线与抛物线方程联立,消去y得x2-(2b+4)x+b2=0,
由△≥0,得b≥-1,这时x1+x2=2b+4,x1x2=b2,
|AB|=4$\sqrt{2}$$\sqrt{b+1}$,又点P到直线AB的距离为d=$\frac{|3-b|}{\sqrt{2}}$,
所以S△ABP=$\sqrt{2(b+1)(3-b)^{2}}$,
令f(x)=(x+1)(3-x)2(x∈[-1,3]),则由f′(x)=(3x-1)(x-3)=0,得x=$\frac{1}{3}$或x=3,
当x∈(-1,$\frac{1}{3}$)时,f′(x)>0,所以f(x)单调递增,当x∈($\frac{1}{3}$,3)时,f′(x)>0,所以f(x)单调递减,
故f(x)的最大值为$\frac{256}{27}$,故△ABP面积S△ABP的最大值为$\frac{16\sqrt{6}}{9}$.
点评 本题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力,以及运算求解能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (-3,2) | C. | (-2,3) | D. | (3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$或$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{12}$=1 | ||
| C. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com