
分析 (1)根据向量的数量积的运算和向量模的计算即可,
(2)根据向量垂直的条件以及向量的夹角公式计算即可.
解答 解:(1)∵向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|$=$|{\overrightarrow b}|$=3,且$\overrightarrow a$与$\overrightarrow b$的夹角为120°,
∴$\overrightarrow a$•$\overrightarrow b$=$|{\overrightarrow a}|$•$|{\overrightarrow b}|$•cos120°=3×3×(-$\frac{1}{2}$)=-$\frac{9}{2}$,
∴$|{\overrightarrow a+\overrightarrow b}|$2=$|{\overrightarrow a}|$2+$|{\overrightarrow b}|$2+2$\overrightarrow a$•$\overrightarrow b$=9+9+2×(-$\frac{9}{2}$)=9,$|{2\overrightarrow a-\overrightarrow b}|$2=4$|{\overrightarrow a}|$2+$|{\overrightarrow b}|$2-4$\overrightarrow a$•$\overrightarrow b$=36+9-4×(-$\frac{9}{2}$)=63,
∴$|{\overrightarrow a+\overrightarrow b}|$=3,$|{2\overrightarrow a-\overrightarrow b}|$=3$\sqrt{7}$;
(2)设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,
∵非零向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a+3\overrightarrow b$与$7\overrightarrow a-5\overrightarrow b$互相垂直,$\overrightarrow a-4\overrightarrow b$与$\overrightarrow{7a}-2\overrightarrow b$互相垂直,
∴($\overrightarrow a+3\overrightarrow b$)•($7\overrightarrow a-5\overrightarrow b$)=0,($\overrightarrow a-4\overrightarrow b$)•($\overrightarrow{7a}-2\overrightarrow b$)=0,
∴7|$\overrightarrow{a}$|2-15|$\overrightarrow{b}$|2+16$\overrightarrow{a}•\overrightarrow{b}$=0,7|$\overrightarrow{a}$|2+8|$\overrightarrow{b}$|2-30$\overrightarrow{a}•\overrightarrow{b}$=0,
∴|$\overrightarrow{b}$|2=2$\overrightarrow{a}•\overrightarrow{b}$,|$\overrightarrow{a}$|2=2$\overrightarrow{a}•\overrightarrow{b}$,
∴|$\overrightarrow{b}$|•|$\overrightarrow{a}$|=2$\overrightarrow{a}•\overrightarrow{b}$,
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{1}{2}$
又θ∈[0,π]
∴θ=$\frac{π}{3}$
点评 本题考查向量的夹角与向量的数量积的关系,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (0,-1) | C. | (0,1) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
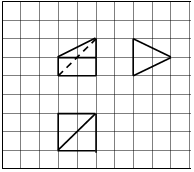 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | 12π | D. | $\frac{41}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2e(x-1) | B. | y=ex-1 | C. | y=e(x-1) | D. | y=x-e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
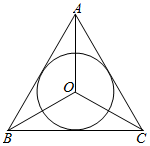 如图:在图O内切于正三角形△ABC,则S△ABC=S△OAB+S△OAC+S△OBC=3•S△OBC,即$\frac{1}{2}•|{BC}|•h=3•\frac{1}{2}•|{BC}|•r$,即h=3r,从而得到结论:“正三角形的高等于它的内切圆的半径的3倍”;类比该结论到正四面体,可得到结论:“正四面体的高等于它的内切球的半径的a倍”,则实数a=( )
如图:在图O内切于正三角形△ABC,则S△ABC=S△OAB+S△OAC+S△OBC=3•S△OBC,即$\frac{1}{2}•|{BC}|•h=3•\frac{1}{2}•|{BC}|•r$,即h=3r,从而得到结论:“正三角形的高等于它的内切圆的半径的3倍”;类比该结论到正四面体,可得到结论:“正四面体的高等于它的内切球的半径的a倍”,则实数a=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$π | B. | $\frac{1}{3}$π | C. | $\frac{1}{2}$π | D. | $\frac{5}{6}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com