
【题目】已知函数![]() .
.
(1)若![]() 在区间
在区间![]() 有最大值,求整数
有最大值,求整数![]() 的所有可能取值;
的所有可能取值;
(2)求证:当![]() 时,
时, ![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)![]() 在区间
在区间![]() 有最大值,即是
有最大值,即是![]() 在区间
在区间![]() 有极大值,求出
有极大值,求出![]() ,求出极大值点
,求出极大值点![]() ,令
,令![]() ,从而可得结果;(2)
,从而可得结果;(2)![]() 等价于
等价于![]() ,只需证明
,只需证明![]() 即可.
即可.
试题解析:(1)f′(x)=(x2+x-2)ex,
当x<-2时,f′(x)>0,f(x)单调递增,
当-2<x<1时,f′(x)<0,f(x)单调递减,
当x>1时,f′(x)>0,f(x)单调递增,
由题知:a<-2<a+5,得:-7<a<-2,
则a=-6、-5、-4、-3,
当a=-6、-5、-4,显然符合题意,
若a=-3时,f(-2)=5e―2,f(2)=e2,f(-2)<f(2),不符合题意,舍去.
故整数a的所有可能取值-6,―5,-4.
(2)f(x)<-3lnx+x3+(2x2-4x)ex+7可变为(-x2+3x-1)ex<-3lnx+x3+7,
令g(x)=(-x2+3x-1)ex,h(x)=-3lnx+x3+7,
g′(x)=(-x2+x+2)ex,
0<x<2时,g′(x)>0,g(x)单调递增,
当x>2时,g′(x)<0,g(x)单调递减,
g(x)的最大值为g(2)=e2,
h′(x)=![]() ,当0<x<1时,h′(x)<0,h(x)单调递减,
,当0<x<1时,h′(x)<0,h(x)单调递减,
当x>1时,h′(x)>0,h(x)单调递增,
h(x)的最小值为h(1)=8>e2,
g(x)的最大值小于h(x)的最小值,
故恒有g(x)<h(x),即f(x)<-3lnx+x3+(2x2-4x)ex+7.


科目:高中数学 来源: 题型:
【题目】二次函数f(x)的图象经过点(0, ![]() ),且f′(x)=﹣x﹣1,则不等式f(10x)>0的解集为( )
),且f′(x)=﹣x﹣1,则不等式f(10x)>0的解集为( )
A.(﹣3,1)
B.(﹣lg3,0)
C.( ![]() ,1)
,1)
D.(﹣∞,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一条公路上,每隔100km有个仓库(如图),共有5个仓库.一号仓库存有10t货物,二号仓库存20t,五号仓库存40t,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输1km需要0.5元运输费,那么要多少才行? ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
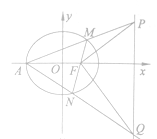
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为该椭圆的右焦点,过点
为该椭圆的右焦点,过点![]() 任作一直线
任作一直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]() 的最大值为4.
的最大值为4.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, ![]() OA为半径作圆.
OA为半径作圆. 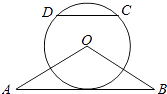
(1)证明:直线AB与⊙O相切;
(2)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且在区间(0,+∞)上是单调递增,若 ![]() ,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,π)
,π)
C.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
D.( ![]() ,
, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照各人带钱多少的比例进行交税,问三人各应付多少税?则下列说法错误的是( )
A. 甲应付![]() 钱 B. 乙应付
钱 B. 乙应付![]() 钱
钱
C. 丙应付![]() 钱 D. 三者中甲付的钱最多,丙付的钱最少
钱 D. 三者中甲付的钱最多,丙付的钱最少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com