Question

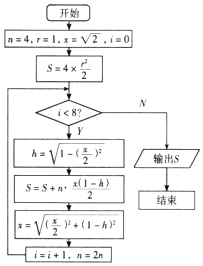
19．我国魏晋时期的数学家刘徽，他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π，用刘徽自己的原话就是“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣．”设计程序框图是计算圆周率率不足近似值的算法，其中圆的半径为1．请问程序中输出的S是圆的内接正（　　）边形的面积．

• A． 1024
• B． 2048
• C． 3072
• D． 1536

Answer 1

分析 模拟程序的运行，可得程序框图的功能是计算并输出当i=8时，n边形的面积S的值，列出循环过程中i与n的数值，即可得解．

解答 解：模拟程序的运行，可得当i=8时，不满足条件i＜8，退出循环，输出S的值．
即程序框图的功能是计算并输出当i=8时，n边形的面积S的值．
由于：i=0时，n=4；
i=1时，n=8；
i=2时，n=16；
…
i=7时，n=512；
i=8时，n=1024；
可得：程序中输出的S是圆的内接正1024边形的面积．
故选：A．

点评 本题考查循环框图的应用，考查了计算能力，注意判断框的条件的应用，属于基础题．