
分析 (1)求解曲线C的直角坐标方程,将直线l的参数方程$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$(t为参数,0≤φ<π),带入,得到关于t的一元二次方程的关系式,由题意判别式大于0,可得φ的取值范围.
(2)利用参数的几何意义即可求线段P1P2中点轨迹的参数方程.
解答 解:(1)曲线C的极坐标方程为ρ=1,根据ρ2=x2+y2可得曲线C的直角坐标方程为x2+y2=1,
将$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$代入x2+y2=1得t2-4tsinφ+3=0(*)
由16sin2φ-12>0,得$|{sinφ}|>\frac{{\sqrt{3}}}{2}$,又0≤φ≤π,
∴所求φ的取值范围是$({\frac{π}{3},\frac{2π}{3}})$;
(Ⅱ)由(1)中的(*)可知,$\frac{{{t_1}+{t_2}}}{2}=2sinφ$,代入$\left\{\begin{array}{l}x=tcosφ\\ y=-2+tsinφ\end{array}\right.$中,
整理:得P1P2的中点的轨迹方程为$\left\{\begin{array}{l}x=sin2φ\\ y=-1-cos2φ\end{array}\right.$(φ为参数,$\frac{π}{3}<φ<\frac{2π}{3}$).
故得线段P1P2中点轨迹的参数方程为为$\left\{\begin{array}{l}x=sin2φ\\ y=-1-cos2φ\end{array}\right.$(φ为参数,$\frac{π}{3}<φ<\frac{2π}{3}$).
点评 本题主要考查了极坐标方程与直角坐标方程的互换和参数方程的几何意义的运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36秒 | B. | 33秒 | C. | 30秒 | D. | 15秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
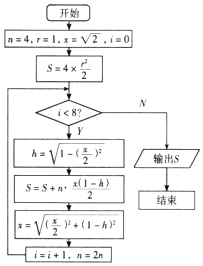 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.| A. | 1024 | B. | 2048 | C. | 3072 | D. | 1536 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com