
分析 (Ⅰ)求出f(x)的导数,设出切点,可得切线的斜率,由两点的斜率公式,解方程可得切点坐标,进而得到所求切线的方程;
(Ⅱ)求出h(x)的解析式和导数,讨论a<0,0<a<1,a≥1,求出极值点和单调区间,由2h(x2)-x1>0等价为2h(x2)+x2>0,由x2=$\sqrt{1-a}$,可得a=1-x22,即证明2(1-x22)ln(x2+1)+x22-x2>0,由0<x2<1,可得1-x2>0,
即证明2(1+x2)ln(x2+1)-x2>0,构造函数t(x)=2(1+x)ln(1+x)-x,0<x<1,求出导数判断单调性,即可得证.
解答 解:(Ⅰ)函数f(x)=ln(x+1)的导数为f′(x)=$\frac{1}{x+1}$,
设切点为(x0,y0),则切线的斜率为k=$\frac{1}{1+{x}_{0}}$,
点(x0,y0)在f(x)=ln(x+1)上,则y0=ln(1+x0),
可得$\frac{ln({x}_{0}+1)}{{x}_{0}+1}$=$\frac{1}{{x}_{0}+1}$,解得x0=e-1,
可得切线的斜率为$\frac{1}{e}$,则切线方程为y-0=$\frac{1}{e}$(x+1),
即为x-ey+1=0;
(Ⅱ)证明:h(x)=af(x)+g(x)=aln(x+1)+$\frac{1}{2}$x2-x,
导数h′(x)=$\frac{a}{1+x}$+x-1=$\frac{{x}^{2}+(a-1)}{x+1}$,x>-1,
当a-1≥0时,即a≥1时,h′(x)≥0,h(x)在(-1,+∞)上单调递增;
当0<a<1时,由h′(x)=0得,x1=-$\sqrt{1-a}$,x2=$\sqrt{1-a}$,
故h(x)在(-1,-$\sqrt{1-a}$)上单调递增,在(-$\sqrt{1-a}$,$\sqrt{1-a}$)上单调递减,
在($\sqrt{1-a}$,+∞)上单调递增;
当a<0时,由h′(x)=0得,x0=$\sqrt{1-a}$,h(x)在(-$\sqrt{1-a}$,$\sqrt{1-a}$)上单调递减,
在($\sqrt{1-a}$,+∞)上单调递增.
当0<a<1时,h(x)有两个极值点,即x1=-$\sqrt{1-a}$,x2=$\sqrt{1-a}$,
可得x1+x2=0,x1x2=a-1,由0<a<1得,-1<x1<0,0<x2<1,
由2h(x2)-x1>0等价为2h(x2)+x2>0,即为2aln(x2+1)+x22-x2>0,
由x2=$\sqrt{1-a}$,可得a=1-x22,即证明2(1-x22)ln(x2+1)+x22-x2>0,
由0<x2<1,可得1-x2>0,
即证明2(1+x2)ln(x2+1)-x2>0,
构造函数t(x)=2(1+x)ln(1+x)-x,0<x<1,
t′(x)=2(1+x)•$\frac{1}{1+x}$+2ln(x+1)-1=1+2ln(1+x)>0,t(x)在(0,1)上单调递增,
又t(0)=0,所以t(x)>0在(0,1)时恒成立,
即2(1+x2)ln(x2+1)-x2>0成立
则2h(x2)-x1>0.
点评 本题考查导数的运用:求切线的方程,注意设出切点,以及极值问题,考查不等式的证明,注意运用分类讨论思想方法和运用导数判断单调性,构造函数是解题的关键,属于难题.


科目:高中数学 来源: 题型:解答题
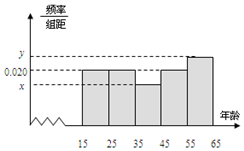 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | c | 0.80 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [-1,1] | C. | (-∞,2] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为增函数 | |
| B. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为增函数 | |
| C. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为减函数 | |
| D. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 5.25 | B. | 5.15 | C. | 5.5 | D. | 9.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com