
| A. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为增函数 | |
| B. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为增函数 | |
| C. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为减函数 | |
| D. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数 |
分析 由两角和的正弦公式化简解析式,由三角函数的奇偶性和诱导公式列出方程,结合条件求出φ的值,由三角函数的周期、余弦函数的单调性得到答案.
解答 解:由题意知,$f(x)=\sqrt{3}sin(2x+φ)+cos(2x+φ)$
=$2[\frac{\sqrt{3}}{2}sin(2x+φ)+\frac{1}{2}cos(2x+φ)]$
=$2sin(2x+φ+\frac{π}{6})$,
∵f(x)是偶函数,∴$φ+\frac{π}{6}=\frac{π}{2}+kπ(k∈Z)$,
则$φ=\frac{π}{3}+kπ(k∈Z)$,
∵$|φ|<\frac{π}{2}$,∴φ=$\frac{π}{3}$,
则$f(x)=2sin(2x+\frac{π}{2})=2cos2x$,
∴f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数,
故选:D.
点评 本题考查两角和的正弦公式、诱导公式,三角函数的奇偶性和周期公式,以及余弦函数的单调性,考查化简、变形能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
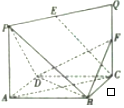 如图,ACQP所在的平面与菱形ABCD所在的平面相互垂直,交线为AC,若$AC=\sqrt{2}AP,E,F$分别是PQ,CQ的中点.求证:
如图,ACQP所在的平面与菱形ABCD所在的平面相互垂直,交线为AC,若$AC=\sqrt{2}AP,E,F$分别是PQ,CQ的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
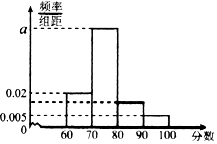 某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [60,70) | 16 | 0.2 |
| [70,80) | 50 | n |
| [80,90) | 10 | P |
| [90,100] | 4 | 0.05 |
| 合计 | M | I |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36秒 | B. | 33秒 | C. | 30秒 | D. | 15秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com