
选修4—4:坐标系与参数方程。
在平面直角坐标系xOy中,已知曲线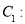
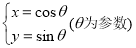 ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.
(1)将曲线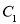 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、2倍后得到曲线
、2倍后得到曲线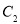 ,试写出直线
,试写出直线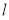 的直角坐标方程和曲线
的直角坐标方程和曲线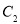 的参数方程;
的参数方程;
(2)在曲线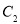 上求一点P,使点P到直线
上求一点P,使点P到直线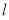 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
科目:高中数学 来源:2016-2017学年河北武邑中学高一上周考9.11数学试卷(解析版) 题型:解答题
已知二次函数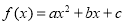 和一次函数
和一次函数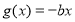 ,其中
,其中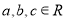 且满足
且满足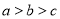 ,
,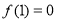 .
.
(Ⅰ)证明:函数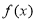 与
与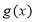 的图像交于不同的两点;
的图像交于不同的两点;
(Ⅱ)若函数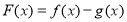 在[2,3]上的最小值为9,最大值为21,试求
在[2,3]上的最小值为9,最大值为21,试求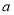 ,
,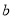 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳五中高三上学期开学考数学(理)试卷(解析版) 题型:选择题
某产品的广告费用 与销售额
与销售额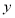 的不完整统计数据如下表:
的不完整统计数据如下表:
广告费用 | 3 | 4 | 5 |
销售额 | 22 | 28 | m |
若已知回归直线方程为 ,则表中
,则表中 的值为
的值为
A. B.39 C.38 D.37
B.39 C.38 D.37
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳五中高三上学期开学考数学(文)试卷(解析版) 题型:选择题
已知定义在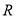 上的函数
上的函数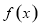 在
在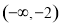 上是减函数,若
上是减函数,若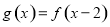 是奇函数,且
是奇函数,且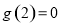 ,则不等式
,则不等式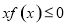 的解集是( )
的解集是( )
A.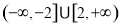 B.
B.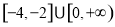
C.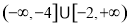 D.
D.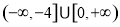
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上学期月考一数学(理)试卷(解析版) 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=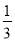 x2+10x(万元);当年产量不少于80千件时,C(x)=51x+
x2+10x(万元);当年产量不少于80千件时,C(x)=51x+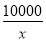 -1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
-1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上学期月考一数学(理)试卷(解析版) 题型:选择题
已知定义在 上的函数
上的函数 满足:函数
满足:函数 的图象关于直线
的图象关于直线 对称,且当
对称,且当 (
( 是函数
是函数 的导函数)成立.若
的导函数)成立.若
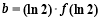 ,
, ,则
,则 的大小关系是
的大小关系是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上学期月考一数学(文)试卷(解析版) 题型:解答题
设 +
+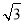 .
.
(1)求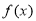 在
在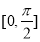 上的最大值和最小值;
上的最大值和最小值;
(2)把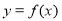 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移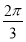 个单位,得到函数
个单位,得到函数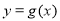 的图象,求g(x)的单调减区间.
的图象,求g(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com