
设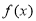 为定义在
为定义在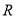 上的奇函数,当
上的奇函数,当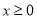 时,
时,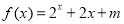 (
(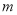 为常数),则
为常数),则 
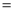 ( )
( )
A.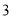 B.
B.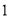 C.
C.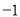 D.
D.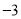
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:填空题
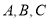 是平面内不共线的三点,点P在该平面内且有
是平面内不共线的三点,点P在该平面内且有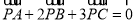 ,现将一粒黄豆随机撒在△
,现将一粒黄豆随机撒在△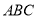 内,则这粒黄豆落在△
内,则这粒黄豆落在△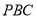 内的概率为__________.
内的概率为__________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
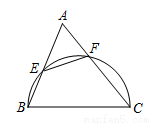
如图,在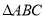 中,以
中,以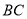 为直径的半圆分别交
为直径的半圆分别交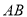 ,
,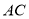 于点
于点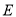 ,
,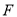 ,且
,且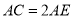 ,那么____;
,那么____; ___.
___.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省协作体第二次适应性测文科数学试卷(解析版) 题型:填空题
.已知双曲线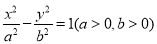 的左右焦点分别为
的左右焦点分别为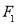 ,
,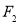 ,
,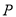 为双曲线右支上的任意一点,若
为双曲线右支上的任意一点,若 的最小值为
的最小值为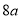 ,则双曲线离心率的取值范围是 。
,则双曲线离心率的取值范围是 。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省协作体第二次适应性测文科数学试卷(解析版) 题型:选择题
在等腰三角形 中,
中,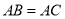 ,
,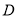 在线段
在线段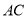 ,
,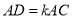 (
(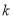 为常数,且
为常数,且 ),
), 为定长,则
为定长,则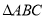 的面积最大值为( )
的面积最大值为( )
A. B.
B. C.
C.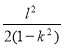 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研文科数学试卷(解析版) 题型:解答题
(本题满分18分)本题共有3个小题,第(1)小题4分,第(2)小题6分,第(3)小题8分
已知函数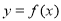 ,若在定义域内存在
,若在定义域内存在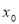 ,使得
,使得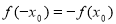 成立,则称
成立,则称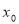 为函数
为函数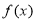 的局部对称点.
的局部对称点.
(1)若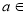 R且
R且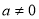 ,证明:函数
,证明:函数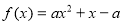 必有局部对称点;
必有局部对称点;
(2)若函数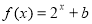 在区间
在区间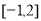 内有局部对称点,求实数
内有局部对称点,求实数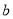 的取值范围;
的取值范围;
(3)若函数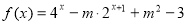 在R上有局部对称点,求实数
在R上有局部对称点,求实数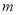 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研文科数学试卷(解析版) 题型:选择题
“点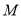 在曲线
在曲线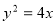 上”是“点
上”是“点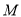 的坐标满足方程
的坐标满足方程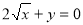 ”的( )
”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研理科数学试卷(解析版) 题型:解答题
已知数列 的前
的前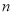 项和为
项和为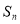 ,且
,且 ,
,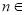 N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知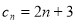 (
(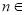 N*),记
N*),记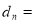
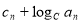 (
(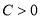 且
且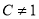 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列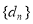 是常数列,若存在,求出
是常数列,若存在,求出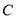 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列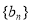 ,对于任意的正整数
,对于任意的正整数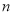 ,均有
,均有 成立,求证:数列
成立,求证:数列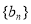 是等差数列;
是等差数列;
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温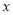 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量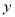 (杯),得到如下数据:
(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程 .
.
(参考公式: .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com