

| A. | 直线A1B与直线AC所成的角是45° | |
| B. | 直线A1B与平面ABCD所成的角是30° | |
| C. | 二面角A1-BC-A的大小是60° | |
| D. | 直线A1B与平面A1B1CD所成的角是30° |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,连结BC1、A1C1,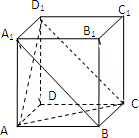
∵在正方体ABCD-A1B1C1D1中,A1A平行且等于C1C,
∴四边形AA1C1C为平行四边形,可得A1C1∥AC,
因此∠BA1C1(或其补角)是异面直线A1B与AC所成的角,
设正方体的棱长为a,则△A1B1C中A1B=BC1=C1A1=$\sqrt{2}$a,
∴△A1B1C是等边三角形,可得∠BA1C1=60°,
即异面直线A1B与AC所成的角等于60°.即A不正确;
直线A1B与平面ABCD所成的角是∠A1BA=45°,即B不正确;
二面角A1-BC-A的平面角是∠A1BA=45°,即C不正确;
因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O为A1B与平面A1B1CD所成的角.设正方体的棱长为a
在RT△A1BO中,A1B=$\sqrt{2}$a,BO=$\frac{\sqrt{2}}{2}$a,所以BO=$\frac{1}{2}$A1B,∠BA1O=30°,
即直线A1B和平面A1B1CD所成的角为30°,即D正确.
故选D.
点评 本题在正方体中求异面直线所成角和直线与平面所成角的大小,着重考查了正方体的性质、空间角的定义及其求法等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 3 | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 测定一批炮弹的射程 | |
| B. | 测定海洋水域的某种微生物的含量 | |
| C. | 高考结束后,国家高考命题中心计算数学试卷中每个题目的难度 | |
| D. | 检测某学校全体高二学生的身高和体重的情况 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要且不充分条件 | B. | 充分且不必要条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com