练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知i是虚数单位，复数z=（a+i）（1-i），若z的实部与虚部相等，则实数a=（　　）
    A．1B．0C．-1D．-2

    分析 利用复数代数形式的乘法运算化简，再由实部与虚部相等求得a值．

    解答 解：∴z=（a+i）（1-i）=a+1+（1-a）i，
    ∴由a+1=1-a，得a=0．
    故选：B．

    点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知半径为2的圆内接三角形的面积为$\frac{1}{4}$，则此三角形三边长的乘积为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

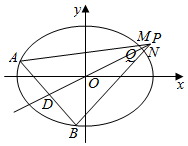    1．如图，已知直线OP交椭圆C：$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1于点Q，其中O为坐标原点，点P的坐标为（2，1），$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$，若椭圆C不经过原点的弦AB被直线OP平分于点D，且直线AP，BP与椭圆C的另一交点分别为M，N．
    （1）求椭圆C的方程；
    （2）试研究直线MN与AB的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．边长为$4\sqrt{2}$的正方形ABCD的四个顶点在半径为5的球O的表面上，则四棱锥O-ABCD的体积是32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，-3），若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥$\overrightarrow{a}$，$\overrightarrow{b}$∥（$\overrightarrow{a}$-$\overrightarrow{c}$），则$\overrightarrow{c}$=（　　）
    A．（-$\frac{7}{4}$，$\frac{7}{8}$）B．（$\frac{7}{2}$，-$\frac{7}{4}$）C．（-$\frac{7}{2}$，-$\frac{7}{4}$）D．（-$\frac{7}{2}$，$\frac{7}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，a，b，c分别为内角A，B，C的对边，3cosA-cos（B+C）=1，a=$\sqrt{15}$，B=$\frac{π}{4}$，则b等于（　　）
    A．$\sqrt{10}$B．3C．2$\sqrt{2}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在空间，下列说法正确的是（　　）
    A．两组对边相等的四边形是平行四边形
    B．四边相等的四边形是菱形
    C．平行于同一直线的两条直线平行
    D．三点确定一个平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在等腰三角形ABC中，∠A=150°，AB=AC=1，则$\overrightarrow{AB}•\overrightarrow{BC}$=（　　）
    A．$-\frac{{\sqrt{3}}}{2}-1$B．$-\frac{{\sqrt{3}}}{2}+1$C．$\frac{{\sqrt{3}}}{2}-1$D．$\frac{{\sqrt{3}}}{2}+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

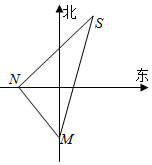    20．如图，一货轮航行到M处，测得灯塔S在货轮的北偏东15°，与灯塔S相距20n mile，随后货轮按北偏西30°的方向航行30min后，又测得灯塔在货轮的东北方向，则货轮的速度为（　　）
    A．20（$\sqrt{2}$+$\sqrt{6}$）n mile/hB．20（$\sqrt{6}$-$\sqrt{2}$）n mile/hC．20（$\sqrt{3}$+$\sqrt{6}$）n mile/hD．20（$\sqrt{6}$-$\sqrt{3}$）n mile/h

    查看答案和解析>>

    同步练习册答案