
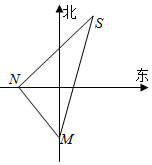
 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |
分析 由题意知SM=20,∠SNM=105°,∠NMS=45°,∠MSN=30°,△MNS中利用正弦定理可得$\frac{MN}{sin30°}$=$\frac{20}{sin105°}$,代入可求MN,进一步利用速度公式即可.
解答 解:由题意知SM=20,∠NMS=45°,
∴SM与正东方向的夹角为75°,MN与正东方向的夹角为,60°
∴SNM=105°
∴∠MSN=30°,
△MNS中利用正弦定理可得,$\frac{MN}{sin30°}$=$\frac{20}{sin105°}$.
MN=$\frac{20×\frac{1}{2}}{\frac{\sqrt{2}+\sqrt{6}}{4}}$=10($\sqrt{6}-\sqrt{2}$)n mile,
∴货轮航行的速度v=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{2}}$=20($\sqrt{6}-\sqrt{2}$) n mile/h.
故选:B.
点评 此题考查了正弦定理在解三角形中的应用,解决实际问题的关键是要把实际问题转化为数学问题,然后利用数学知识进行求解.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
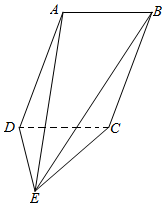 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com