
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
分析 求出导数,求出单调区间,求出极值,曲线f(x)与x轴仅有一个交点,可转化成f(x)极大值<0或f(x)极小值>0即可.
解答 解:函数f(x)=x3-x2-x+a的导数为f′(x)=3x2-2x-1,
当x>1或x<-$\frac{1}{3}$时,f′(x)>0,f(x)递增;
当-$\frac{1}{3}$<x<1时,f′(x)<0,f(x)递减.
即有f(1)为极小值,f(-$\frac{1}{3}$)为极大值.
∵f(x)在(-∞,-$\frac{1}{3}$)上单调递增,
∴当x→-∞时,f(x)→-∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞,
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点.
即a+$\frac{7}{25}$<0或a-1>0,
∴a∈(-∞,-$\frac{7}{25}$)∪(1,+∞),
故选:D.
点评 本题主要考查了利用导数研究函数的极值,以及函数的单调性,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{11\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{21}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
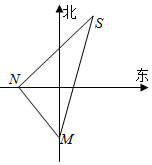 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com