
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |
分析 利用两角和与差的余弦函数化简求解即可.
解答 解:sin(θ-$\frac{π}{3}$)=$\frac{1}{3}$,0<θ<π,cos(θ-$\frac{π}{3}$)=$\frac{2\sqrt{2}}{3}$,(θ-$\frac{π}{3}$∈(0,$\frac{π}{6}$)).
cosθ=cos[(θ-$\frac{π}{3}$)+$\frac{π}{3}$]=cos(θ-$\frac{π}{3}$)cos$\frac{π}{3}$-sin(θ-$\frac{π}{3}$)sin$\frac{π}{3}$=$\frac{2\sqrt{2}}{3}×\frac{1}{2}-\frac{1}{3}×\frac{\sqrt{3}}{2}$=$\frac{-\sqrt{3}+2\sqrt{2}}{6}$.
故选:A.
点评 本题考查两角和与差的三角函数化简求值,考查计算能力.


科目:高中数学 来源: 题型:解答题
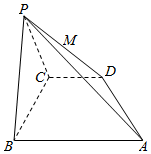 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | B⊆A | B. | A∪B=A | C. | A∩B=B | D. | A∩B={3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com