
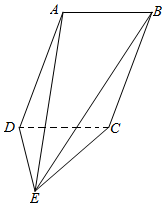
 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE分析 (Ⅰ)过A作AH⊥DC交DC于H.证明AH⊥DE,AD⊥DE,然后证明DE⊥平面ABCD;
(Ⅱ)过C作CM⊥AD交AD于M,过C作CN⊥AE交AE于N,连接MN.说明∠CNM就是所求二面角的一个平面角.然后求解即可.
解答 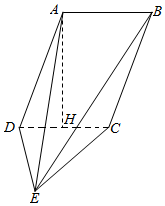 (本题满分15分)
(本题满分15分)
证明:(Ⅰ)过A作AH⊥DC交DC于H.
∵平行四边形ABCD⊥平面CDE
∴AH⊥平面CDE
又∵DE?平面CDE
∴AH⊥DE…①由已知AD⊥DE…②,AH∩AD=A…③
由①②③得,DE⊥平面ABCD; …(7分)
解:(Ⅱ)过C作CM⊥AD交AD于M,过C作CN⊥AE交AE于N,
连接MN.
由(Ⅰ)得DE⊥平面ABCD,
又∵DE?平面ADE,
∴平面ADE⊥平面ABCD.
∴CM⊥AE,
又∵CN垂直AE,且CM∩CN=C.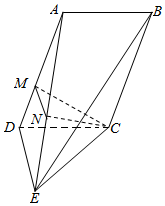
∴AE⊥平面CMN,得角CNM就是所求二面角的一个平面角.
又∵$CM=2\sqrt{3}$,$MN=\sqrt{2}$,
∴所求二面角的余弦值为$\frac{{\sqrt{7}}}{7}$.…(8分)
点评 本题考查二面角的平面角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{7}{4}$,$\frac{7}{8}$) | B. | ($\frac{7}{2}$,-$\frac{7}{4}$) | C. | (-$\frac{7}{2}$,-$\frac{7}{4}$) | D. | (-$\frac{7}{2}$,$\frac{7}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{{e}^{2}}$,$\frac{1}{2e}$) | B. | [$\frac{1}{2e}$,$\frac{1}{e}$] | C. | (0,$\frac{1}{{e}^{2}}$) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{11\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{21}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
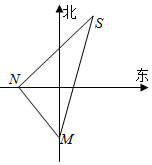 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com